About Us
Executive Editor:Publishing house "Academy of Natural History"
Editorial Board:
Asgarov S. (Azerbaijan), Alakbarov M. (Azerbaijan), Aliev Z. (Azerbaijan), Babayev N. (Uzbekistan), Chiladze G. (Georgia), Datskovsky I. (Israel), Garbuz I. (Moldova), Gleizer S. (Germany), Ershina A. (Kazakhstan), Kobzev D. (Switzerland), Kohl O. (Germany), Ktshanyan M. (Armenia), Lande D. (Ukraine), Ledvanov M. (Russia), Makats V. (Ukraine), Miletic L. (Serbia), Moskovkin V. (Ukraine), Murzagaliyeva A. (Kazakhstan), Novikov A. (Ukraine), Rahimov R. (Uzbekistan), Romanchuk A. (Ukraine), Shamshiev B. (Kyrgyzstan), Usheva M. (Bulgaria), Vasileva M. (Bulgar).
Materials of the conference "EDUCATION AND SCIENCE WITHOUT BORDERS"
Cases when some input data is unknown arise when solving mathematical models. There are many ways to disclose uncertainties but the most appropriate way is interval analysis since it uses interval numbers which contain minimal information about uncertain parameters.
The uncertainty parameter ![]() is specified as an interval parameter (interval number):
is specified as an interval parameter (interval number):
![]() ,
, ![]()
where ![]() are the lower and upper boundaries of parameters
are the lower and upper boundaries of parameters ![]() ;
; ![]() is class mark
is class mark ![]() (fig. 1):
(fig. 1):
![]() ; (1)
; (1)
value ![]() is the interval which is determined by:
is the interval which is determined by:
![]() . (2)
. (2)
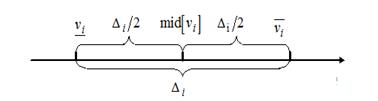
Fig.1. Image of interval parameter on the number scale
Mathematical models with such parameters are called interval models. Let’s define an interval mathematical model in the form of an operator [1]:
![]() (3)
(3)
where ![]() - interval vectors, defined as:
- interval vectors, defined as: ![]() ,
, ![]() ;
;
X – space of input values, U - space of admissible control effects, Y - space of output values, V - the space of uncertain parameters.
To solve the problems of design and process control it is required to find an interval vector of the output parameters ![]() of the mathematical model (3).
of the mathematical model (3).
To solve the interval mathematical model ![]() , means for a given vector
, means for a given vector ![]() interval vector
interval vector ![]() to find a vector
to find a vector ![]() that is defined by the vector of lower and upper boundaries
that is defined by the vector of lower and upper boundaries![]() ,
, ![]() .
.
According to the classification [2], mathematical models of processes are divided into static and dynamic models, which in their turn are classified into models with lumped and distributed parameters, i.e. into four classes of mathematical models. Each class has its own algorithm for solving the interval model.
This method has been implemented in the firing process in a rotary furnace taken as an example. Rotary furnace is a cylindrical industrial furnace with a rotational movement around its longitudinal axis, designed for heating or burning materials with the aim of their physic-chemical treatment. To maintain the temperature flaring of natural gas or fuel oil is applied. The material in the furnace moves forward flow to the products of combustion [3].
We have developed a mathematical model of the firing process in a rotary furnace:
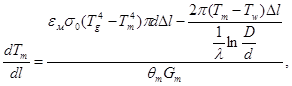 (4)
(4)
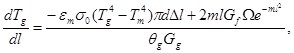 (5)
(5)
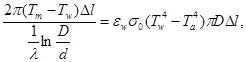 (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
where ![]() - temperature of the material [K],
- temperature of the material [K], ![]() - gas temperature [K],
- gas temperature [K], ![]() - wall temperature [K],
- wall temperature [K], ![]() - ambient temperature [K],
- ambient temperature [K], ![]() - the current length of the furnace [m],
- the current length of the furnace [m],![]() - the emissivity of the lining,
- the emissivity of the lining, ![]() - the emissivity of the material,
- the emissivity of the material,![]() - the inner furnace diameter [m],
- the inner furnace diameter [m],![]() - outer furnace diameter [m],
- outer furnace diameter [m], ![]() - the total length of the furnace [m],
- the total length of the furnace [m],![]() - ratio of blackbody radiation [W/m2K4],
- ratio of blackbody radiation [W/m2K4], ![]() - thermal conductivity of the lining material [W/mK],
- thermal conductivity of the lining material [W/mK], ![]() - the heat from 1 kg of fuel combustion (specific heat of combustion) [J/kg],
- the heat from 1 kg of fuel combustion (specific heat of combustion) [J/kg], ![]() - heat capacity of the material [J/kg℃],
- heat capacity of the material [J/kg℃],
![]() - gas heat capacity [J/kg℃],
- gas heat capacity [J/kg℃],![]() - material consumption [kg/s],
- material consumption [kg/s], ![]() - gas consumption [m3/s],
- gas consumption [m3/s], ![]() - fuel consumption [m3/s],
- fuel consumption [m3/s], ![]() - empirical coefficient.
- empirical coefficient.
This mathematical model has uncertain parameters. This is the emissivity of the material![]() , the heat capacity of the material
, the heat capacity of the material ![]() and the length of the torch
and the length of the torch ![]() . Empirical coefficient
. Empirical coefficient ![]() depends on the length of the torch, thus changing the length of the flare leads to a change in the empirical coefficient.
depends on the length of the torch, thus changing the length of the flare leads to a change in the empirical coefficient.
A mathematical model of the firing process in a rotary furnace belongs to a class of static models with distributed parameters.
Uncertain parameters of the mathematical model are given in the form of interval numbers:
![]() = [0.3, 0.7],
= [0.3, 0.7], ![]() = [1000, 1200],
= [1000, 1200], ![]() = [7, 15]. In the mathematical model the output parameters are: temperature distribution of gas, material and wall along the length of the furnace. The most important parameter for the firing process is the temperature of the material; therefore, all calculations have been performed only for the temperature of the material.
= [7, 15]. In the mathematical model the output parameters are: temperature distribution of gas, material and wall along the length of the furnace. The most important parameter for the firing process is the temperature of the material; therefore, all calculations have been performed only for the temperature of the material.
To solve the model is to calculate the upper and lower boundaries of the entire interval of the temperature distribution of the material (Fig.2).
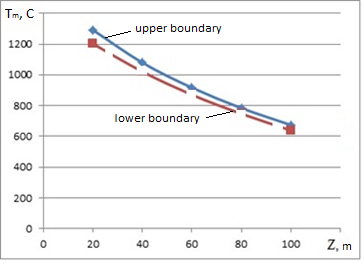
Fig.2. The boundaries of the temperature distribution of the material
The proposed method allows to calculate the interval of output values of mathematical models, which makes it advantageous over other methods of disclosing the uncertainty in mathematical models.
2. Dobre, Tanase Gh. Chemical Engineering: Modelling, Simulation and Similitude / Tanase Gh. Dobre, Jose G. Sanchez Marcano. – Weinheim: Wiley-VCH, 2007. – 568 p.
3. Лисиенко, В.Г. Вращающиеся печи: теплотехника, управление и экология: Справочное издание в 2-х книгах. Книга 2 / В.Г. Лисиенко, Я.М. Щелоков, М.Г. Ладыгичев.- М: Теплотехник, 2004.-592с.
Frolova Tatyana, Dmitry Tulyakov, Sergej Frolov MATHEMATICAL MODEL OF HEAT TRANSFER PROCESS WITH UNCERTAIN PARAMETERS. International Journal Of Applied And Fundamental Research. – 2013. – № 2 –
URL: www.science-sd.com/455-24166 (16.04.2024).











 PDF
PDF