About Us
Executive Editor:Publishing house "Academy of Natural History"
Editorial Board:
Asgarov S. (Azerbaijan), Alakbarov M. (Azerbaijan), Aliev Z. (Azerbaijan), Babayev N. (Uzbekistan), Chiladze G. (Georgia), Datskovsky I. (Israel), Garbuz I. (Moldova), Gleizer S. (Germany), Ershina A. (Kazakhstan), Kobzev D. (Switzerland), Kohl O. (Germany), Ktshanyan M. (Armenia), Lande D. (Ukraine), Ledvanov M. (Russia), Makats V. (Ukraine), Miletic L. (Serbia), Moskovkin V. (Ukraine), Murzagaliyeva A. (Kazakhstan), Novikov A. (Ukraine), Rahimov R. (Uzbekistan), Romanchuk A. (Ukraine), Shamshiev B. (Kyrgyzstan), Usheva M. (Bulgaria), Vasileva M. (Bulgar).
Main peculiarity of optimal control for metal heating in a continuous furnace [1] is that desired solution must respond to several partial optimization criteria depending on situation during the functioning of a furnace. At calculation of optimal modes for slab heating it is proposed to use method of successive concessions which consists in optimization of partial criteria in order of their relative significance with simultaneous assignment of allowable concession, e.g. interval, in which values of previous criterion can vary. As a result minimum of last criterion by significance must be secured on condition that value of each previous criterion must differ from its minimal value not larger than on magnitude of concession.
In heat engineering laboratory of Volgograd metallurgical plant “Red October” full-scale experiments on heating of stocks in continuous furnaces had been carried out. In terms of experiment results processing the objective functions have been determined. These functions characterize partial optimization criteria: ΔTex –difference of temperatures on stock thickness at the exit from the furnace, °C; b – specific fuel rate for furnace, kg e.f./t; δ – losses of metal at the expense of scaling processes, % [2]:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
where x1, x2, x3 – control parameters, dependent proportionally with temperature setpoints of furnace zones.
Also the set of constraints has been formed in terms of above mentioned experimental data:
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
At every step of optimization problem solution the objective functions (1-3) are minimized. Aside from constraints (4-6) at solution of linear programming problem natural constraints on values of control parameters x1>0, x2>0, x3>0 and constraints on maximal values of partial optimization criteria have been used. The second constraints have been chosen taking into account technological requirements to quality of stocks heating in continuous furnaces which had been conditioned on practical training at “Red October”. Before calculation values of concessions on each criterion must be set. These values are stored in database of automatized slab heating control system [3].
At each step of successive concessions method minimization of values for partial criteria has been executing in Microsoft Excel by means of the Solver add-in. The next order of criteria’s relative significance has been chosen: ΔTex, b, δ. The scheme of the algorithm for optimal modes calculation of slab heating in terms of combination of successive concessions method and linear programming problem is represented in figure 1.
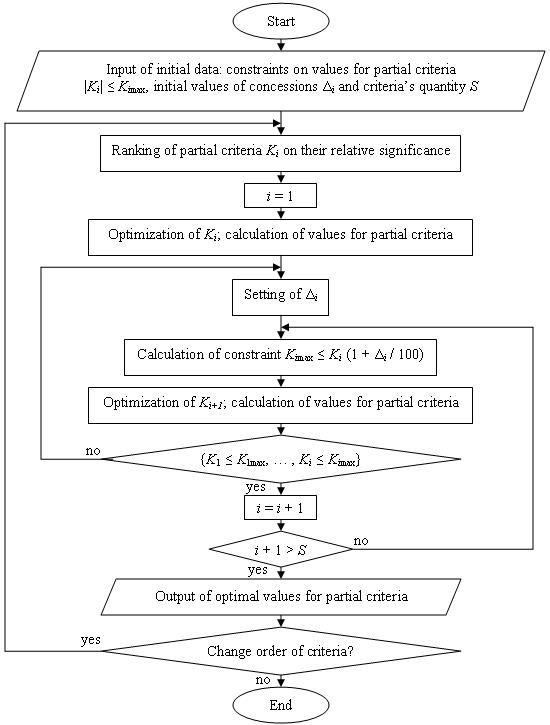
Figure 1 – Algorithm of optimal modes calculation for slab heating
At changing of partial criteria’s order or concessions’ values’ correction re-calculation of optimal values is made. As a result of optimization problem solution for the case of furnace full charge with slabs relating to 1st heating group according to “Red October” nomenclature the values of control parameters have been obtained. These values secure achievement of optimal values for the objective functions: ΔTex = 14,7 °C, b = 72,2 kg e.f./t, δ = 1,46 %. In terms of these parameters’ values the optimal setpoints of furnace zones has been calculated: temperature of first heating zone – 1230 °C, temperature of second heating zone upper part – 1310 °C, temperature of second heating zone lower part – 1280 °C.
Setting these values in boundary conditions of the developed model for temperature field of continuous furnace operating space [4], it is possible to reconstitute optimal modes of heating and to analyze impact of these modes on temperature distribution throughout all volume of furnace operation space.
2. Serdobintsev, Y. P. The choice of a complex criterion of heating process optimization in a continuous furnace / Y. P. Serdobintsev, M. P. Kukhtik, K. F. Kuadio // Proceedings of VSTU: Interuniversity Coll. of Scient. Art. Ser. "Progressive Technologies in Machine Building". – Vol. 9, No. 7. – pp. 111-113.
3. Serdobintsev, Y. P. Automatized slab heating control system in a continuous furnace / Y. P. Serdobintsev, M. P. Kukhtik // International Journal of Applied and Fundamental Research. – 2013. – № 2. – Mode of access : http://www.science-sd.com/455-24314
4. Kukhtik, M. P. Creation of a finite element model for temperature field of continuous furnace operating space in mathematical package COMSOL Multiphysics [Electronic resource] / M. P. Kukhtik // Modern problems of science and education: electronic scientific magazine. – 2012 . – No. 2. – Access mode : http://www.science-education.ru/102-5937
Serdobintsev Y. P., Kukhtik M. P. ALGORITHM OF OPTIMAL MODES CALCULATION FOR SLAB HEATING IN A CONTINUOUS FURNACE. International Journal Of Applied And Fundamental Research. – 2014. – № 2 –
URL: www.science-sd.com/457-24551 (20.01.2026).











 PDF
PDF