A One-Compartment Model

1. The Mass Transport in the Dialyzer

In most of the common dialyzers (called artificial kidneys) the removal of toxical substances from the blood is achieved by extracting it from the body and introducing it into the interior of a kidney machine where it floats along one side of a membrane as being schematically shown in Figure 2.

                                                              Blood             

                                                                  Dialysate

Fig. 1. Blood and Dialysate Flow in the Dialyzer.

At the  same time a dialysate fluid floats along the other side of the membrane in the opposite direction. In the course of this process a mass transport of the toxical substance across the membrane takes place which is based on two mechanisms. The first is diffusion by which the molecules of the substance are pressed through the pores of the membrane under the influence of the difference  of the concentration CB [mg/ml] and  [mg/ml] of the toxical substance in the blood and the dialysate fluid, respectively. The flux  [mg/min] of the substance across the membrane from the blood into the dialysate fluid caused by diffusion is given, according to Fick's law, by

where  [ml/min] is the diffusive clearance of the membrane which can be expressed by

where A is the area of the membrane and [сm/min] is the mass transfer coefficient (this law holds for thin membranes).

The second mechanism of mass transport across the membrane is called ultrafiltration and is caused by a pressure difference between the blood water and the dialysate fluid. This pressure difference gives rise to a blood water flow through the membrane by which dissolved parts of the toxical substance are  transported.

2. The Temporal Development of the Toxin Concentration in the Blood without Ultrafiltration

Let  [ml] be the total blood volume of the patient at the time t. Then the total amount of the toxical substance in the blood at the time t by  is given  [mg/ml].

 We assume that some rest clearance  [ml/min] of the kidneys of the patient is present such that there is a permanent flux Fr [mg/min] of the toxical substance out of the blood across the kidneys into the urine which is of the form   

We further assume that, within a given time interval [0, T] the patient is at­tached to a dialyzer during the time interval [0, td] where td < T.

Then we have,

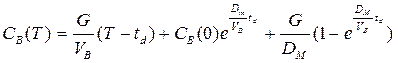
and the requirement turns out to be equivalent to

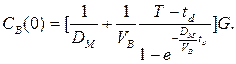
For    we again choose the value 150 [mg/min] and for  the value 13600 [ml].

Then we obtain

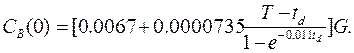
If we assume, that dialysis is performed every second day, i.e., if we put T = 48h=2880 min, then for

the following values are obtained

The mathematical model of process of a hemodialysis is programmatically simualted:

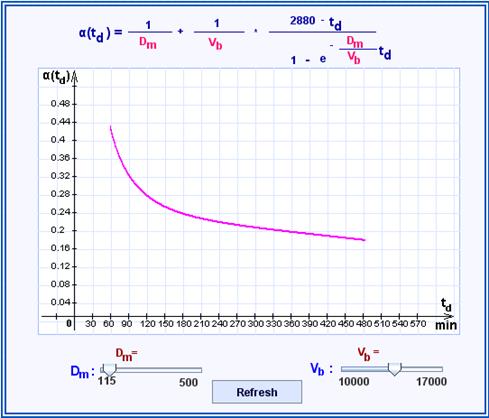
Now we deduce

where

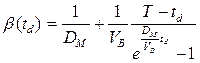
For the above values of  and T we get

which leads to the table

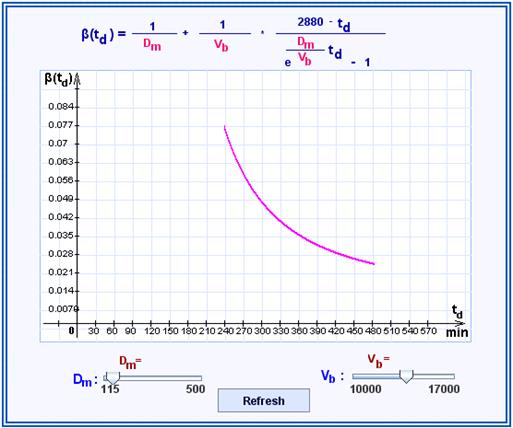
If we define the dialysis effect by

 then we obtain the following table

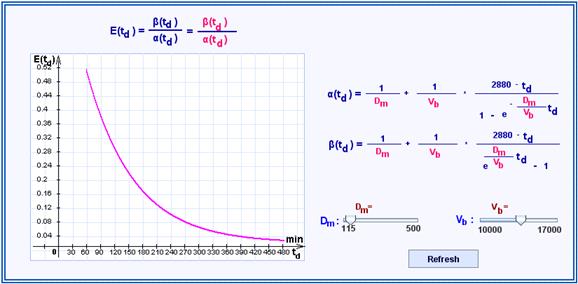
The numerical values in the above tables are not really realistic. Therefore, the one-compartment model will be given up in the following. Nevertheless, they already indicate a tendency (to be confirmed in the refined model lateron), namely, that by extending the durance of dialysis to large times td (beyond 7h) the dialysis effect is only slightly improved. The dialysis effect can now also expressed in the form

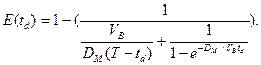
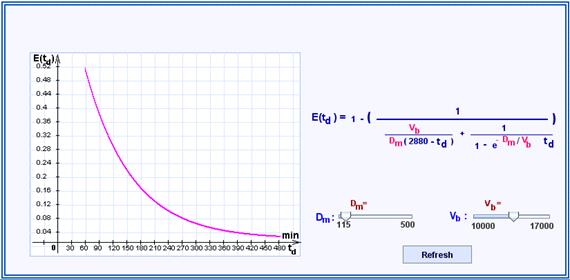
This formula shows immediately that, for fixed values of  and , the value of  decreases, if increases. This is to be expected in the same way as a decrease of , if  is increased where  , and  are kept fixed.