About Us
Executive Editor:Publishing house "Academy of Natural History"
Editorial Board:
Asgarov S. (Azerbaijan), Alakbarov M. (Azerbaijan), Aliev Z. (Azerbaijan), Babayev N. (Uzbekistan), Chiladze G. (Georgia), Datskovsky I. (Israel), Garbuz I. (Moldova), Gleizer S. (Germany), Ershina A. (Kazakhstan), Kobzev D. (Switzerland), Kohl O. (Germany), Ktshanyan M. (Armenia), Lande D. (Ukraine), Ledvanov M. (Russia), Makats V. (Ukraine), Miletic L. (Serbia), Moskovkin V. (Ukraine), Murzagaliyeva A. (Kazakhstan), Novikov A. (Ukraine), Rahimov R. (Uzbekistan), Romanchuk A. (Ukraine), Shamshiev B. (Kyrgyzstan), Usheva M. (Bulgaria), Vasileva M. (Bulgar).
Engineering
Wind turbine torque
Consider
the scheme of counterclockwise rotation of one of the working blades of the wind
turbine with a certain angular velocity"![]() " in Figure 1. Each of
the positions shown in Figure 1 corresponds to the rotation of the blade at
different angles "
" in Figure 1. Each of
the positions shown in Figure 1 corresponds to the rotation of the blade at
different angles "![]() ". Lifting power appears
if wind flux leaks to the rotating turbine at a certain rate "
". Lifting power appears
if wind flux leaks to the rotating turbine at a certain rate "![]() ". In fact, during the
rotation of the turbine the air environment leaks to the blade at a speed equal
to the linear speed of rotation of the latter (
". In fact, during the
rotation of the turbine the air environment leaks to the blade at a speed equal
to the linear speed of rotation of the latter (![]() ). By constructing a vector
parallelogram from velocities
). By constructing a vector
parallelogram from velocities![]() and
and ![]() it is easy to find the
resultant vector
it is easy to find the
resultant vector ![]() - speed of attack and
angle of attack "
- speed of attack and
angle of attack "![]() "
"
![]() =
=![]()
![]()
![]()
![]() , (1)
, (1)
where ![]() - specific speed of the
turbine [1,2].
- specific speed of the
turbine [1,2].
To determine the angle of attack the law of tangents should
be used and inserting ![]() we will
receive
we will
receive
![]() . (2)
. (2)
The (1) and (2) formulas results the very important connections
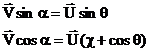 .
(3)
.
(3)
The (1) - (3) formulas allow come to the following conclusions:
а) as the lifting power ![]() is always directed normally to
the
is always directed normally to
the ![]() attack speed, it is only in
the positions "A" and "C" (see Fig. 3) the lifting power is
absent because sinq=0 and tga=0 at all other q angles the "pulling"
force, equal to
attack speed, it is only in
the positions "A" and "C" (see Fig. 3) the lifting power is
absent because sinq=0 and tga=0 at all other q angles the "pulling"
force, equal to ![]() is applied to the blade;
is applied to the blade;
b) the
greatest value ![]() occurs when the blades pass
the points "B" and “D”;
occurs when the blades pass
the points "B" and “D”;
c) a pair of blades arranged symmetrically about
the axis of rotation, lead to occurrence of a force couple (+![]() ) and (-
) and (-![]() ), creating a torque which increases when the blade is moved from the
point "A" to point "B", and decreases from "B" to
"C" (subsequently on the opposite side of the blade the moment of force increases from point "C" to
point “D”, and then decreases to point "A").
), creating a torque which increases when the blade is moved from the
point "A" to point "B", and decreases from "B" to
"C" (subsequently on the opposite side of the blade the moment of force increases from point "C" to
point “D”, and then decreases to point "A").
Lifting
force of the ![]() airfoil is directed
perpendicular to the
airfoil is directed
perpendicular to the ![]() attack velocity vector and is determined with
the formula [3]
attack velocity vector and is determined with
the formula [3]
![]() , (4)
, (4)
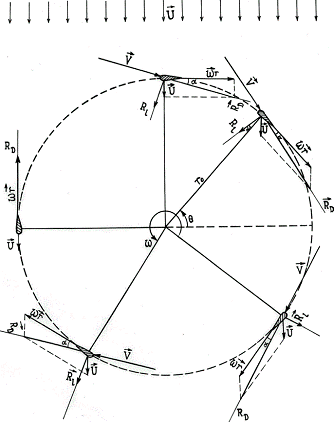 |
Figure 1. The scheme of one of the working wind turbine blades rotating counterclockwise.
where L –length
of blade of a symmetric profile with a chord equal to b, ![]() - lift force coefficient.
- lift force coefficient.
The rotational moment is created by the tangential component of the lifting force, which is designed on the section chord line, or what is the same, on a tangent to the circumference of the movement of the blade:
![]() .
(5)
.
(5)
A part of this force compensates for the resistance force of air to the movement of the blade, which can be written as the following dependence
![]() , (6)
, (6)
where ![]() - resistance coefficient of the
airfoil. Thus, the joint moment that acts on the blade is equal to
- resistance coefficient of the
airfoil. Thus, the joint moment that acts on the blade is equal to
![]() (7)
(7)
or ![]() . (8)
. (8)
where r0 - distance from the axis of rotation to the blade substantially equal to the length of strides.
Due to
the fact that symmetrical working blades were used in our study and the strokes
connecting them to the rotation shaft are made in the form of NASA 0021 symmetrical
airfoils, the ![]() and
and ![]() coefficients of these profiles
in the range of
coefficients of these profiles
in the range of ![]() are well described by
dependencies
are well described by
dependencies
![]() (9)
(9)
![]() (10)
(10)
Substituting the last expression to (8), we obtain
![]() (11)
(11)
Factorizing ![]() from the square
brackets, taking into account (1) and (3), and rewrite as follows:
from the square
brackets, taking into account (1) and (3), and rewrite as follows:
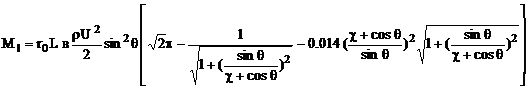 (12)
(12)
If we
take into account that the preferred values of the coefficient of wind energy (x)
of the Darrieus turbine are in the range of ![]() (see. Figure 4). In this
case, at the nominal work of the Darrieus wind turbine the value of
(see. Figure 4). In this
case, at the nominal work of the Darrieus wind turbine the value of ![]() << 1. The latter allows
expanding the elements with radical expression in powers in small parameter and
limiting with first two elements:
<< 1. The latter allows
expanding the elements with radical expression in powers in small parameter and
limiting with first two elements:
![]() .
.
Thus, in the case of two-bladed Darrieus turbine with straight working blades the moment generated by the pair of forces will be expressed by the equation
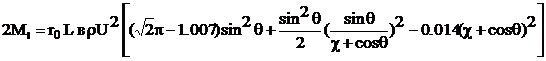 (13)
(13)
Following
evaluation, it must be concluded that the second element in square brackets is
the share of interest from the other two elements, and can be neglected. As a
result, the moment of couple of forces depending on the rotation angle of the
turbine (![]() )for
)for ![]() will be of the form
will be of the form
![]() . (14)
. (14)
Full torque of two-bladed Darrieus wind turbine per one turn will be
found by integrating relation (14) from
0° to 2![]()
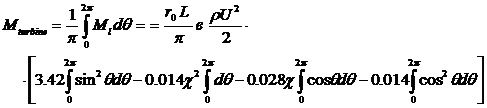
![]()
So, in the final form we will obtain
![]() . (15)
. (15)
These data indicate that the torque that is developing by the lifting force is much higher than resistance force to the air environment to the movement of the blades.
Determination of wind power and energy efficiency
Capacity
of the wind turbine will be determined by multiplying ![]() by its angular velocity
by its angular velocity
![]() =
=![]() . (16)
. (16)
On the other hand it is known that the power of the turbine can be determined, if the value of the wind power efficiency (see Fig. 2) and disk area F are given. In the case the two-bladed Darrieus turbine under consideration F=2pr0L. Hence we have [1]
![]() =
=![]() .
.
Equating the last two relations to each other, we will find
![]() .
.
Typically,
the ratio ![]() . Hence
. Hence
![]() .
.
Equating
the first derivative ![]() on
on ![]() to zero, we will define the
maximum value
to zero, we will define the
maximum value ![]() and the
and the ![]() value at which
value at which![]() is achieved,
is achieved,
![]()
or ![]() , then
, then ![]()
![]() .
.
As can
be seen from the values obtained, ![]() and
and ![]() at which the maximum value of the wind
power efficiency, they are not much different from their experimental values
(see. x(c) influence curve for the Darrieus wind turbine
in Figure 2).
at which the maximum value of the wind
power efficiency, they are not much different from their experimental values
(see. x(c) influence curve for the Darrieus wind turbine
in Figure 2).
The deviation of the theoretical values of x parameter from the experimental ones, apparently is due to the fact that the additional resistance associated with dragging of bearings, the presence of two strokes etc., as well as the decrease in the flow rate at the treatment of the blade in the downwind area (СDА semicircle (see Fig. 2) did not take into account while the calculation
Dependence of the wind power efficiency x for different types and designs of wind turbines on their degree of rapidity c [4].

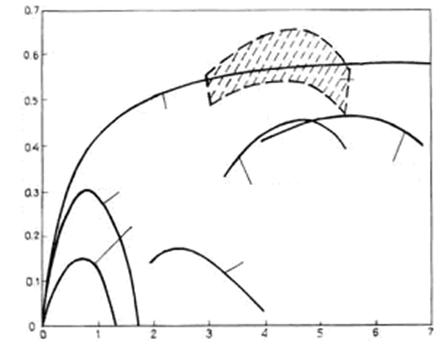
Figure 2. Dependencies of wind power utilization factor x for different types and constructions of wind turbine on the degree of their specific speed c.
2. Yershina A.K., Yershin Sh.A., Zhapbasbayev U.K. Principles of a Darrie wind turbine theory. Almaty, – 104 p, 2001. (in Russian).
3. Loitsyanskii L.G. Mechanics of fluids. M., 1970. 904 p. (in Russian).
4. Turyan CJ., J. Strickland, H., Berg D.E. The power of wind-electric units with a vertical-axis rotation. Aerospace techniques. №8.- pp. 105-121. 1988. (in Russian).
Ainakul K. Yershina ON AERODYNAMICS OF DARIUS WIND TURBINE WITH STRAIGHT BLADES. International Journal Of Applied And Fundamental Research. – 2014. – № 2 –
URL: www.science-sd.com/457-24632 (17.11.2025).











 PDF
PDF