The woody body contains nanocapillary wood in a basis.

Basic data. Basic data are given in table 1 for modeling.

Results [1, page 74] become primary for studying of nanocapillary wood.

Choice of the law of distribution. In the beginning the formula of the indicative law was chosen. However further this hypothesis wasn't confirmed.

Therefore we choose the second option – fragments with background of the studied phenomenon or process [4]. By the form arrangements of points search of parameters of model  is carried out on a hypothesis: at  will be . Then future biotechnical regularity will submit to the exponential law of growth. Other options aren't present therefore, proceeding from the second hypothesis, and we will look for the general formula.

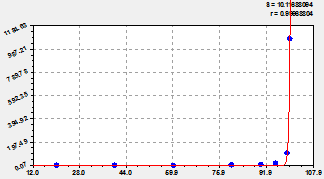
Therefore the trend will register in the form of formula (fig. 1)

     .                                                      (1)

Fig. 1. Trend schedules (at the left) and models with two members (on the right)

The formula (1) possesses remarkable property and shows that at aspiration of relative pressure of water vapor to zero the radius of a capillary of wood will be equal to  nanometer (5,2452e-118 m).

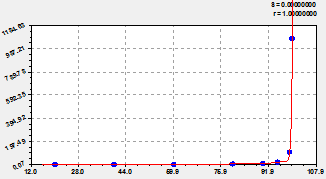
Wave function. After association of a trend with wave function [2-4] the general model [3, 4] which, because of effect of consolidation at "shake-up", is more adequate to experimental basic data is formed.

Abnormally changing biotechnical law [2-4] appeared in a fluctuation amplitude formula (fig. 1, on the right) on a formula

   ,              (2)

, ,

where  - amplitude (half) of fluctuation, nanometer,  - a fluctuation half-cycle, %.

The equation (2) shows that under a condition  it turns out . It is almost difficult to achieve zero depression of air (water vapor) in wood capillaries.

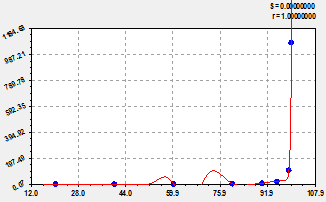
Model building.  Each wave component is supplemented to the previous model.  Then identification of an asimmerichny wavelet signal [4] is again carried out.

The schedule (fig. 2) turns out in the form of a tripartite formula

                                                      ,                                                                   (3)

, ,

, ,

, ,

.

Fig. 2. Schedules of trinomial model (3) and the remains from it (on the right)

Because of small quantity of experimental points in figure 2 the schedule received ledges. Therefore it is an example has only methodical character.

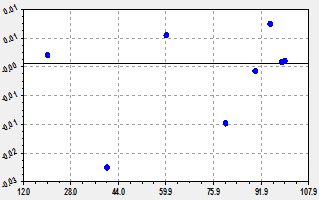
Modeling error. On a trend with two waves of the calculations are given in table 2.

So, the maximum relative error of trinomial statistical model (3) is equal only 1,86%. And this error was displaced towards reduction of radius of a capillary.

Conclusion. Wood possesses nanostructure. The concretization of spatial distribution of nanocages distinguishes dendrometric approach from a wood science existing in Russia. In this regard the main task by consideration of wood of a growing tree is creation of digital model on separate properties of wood [2].

At increase in number of data on table 1 and increase of accuracy of measurements the statistical model with a large number of members is possible. On our methodology [2-4] it is possible to bring number of members of the general model to several tens. However, that the effect of consolidation "shake-up" was always, it is necessary to create according to our scenarios the new program environment for the supercomputer, sharply reducing labor input of modeling.

2. Mazurkin P. M. Dendrometry. Statistical studying of a tree: manual H. 2. Yoshkar-Ola: MarSTU, 2003. 205 pages.

3. Mazurkin P.M. Analisi dendrocronologica series. Italian Science Review. 2014; 5(14). PP. 163-169. Available at URL: http://www.ias-journal.org/archive/2014/may/Mazurkin.pdf.

4. P.M. Mazurkin. Statistical modeling of entire prime numbers / International Journal of Engineering and Technical Research (IJETR) ISSN: 2321-0869, Volume-2, Issue-8, August 2014. Р.148-158.