About Us
Executive Editor:Publishing house "Academy of Natural History"
Editorial Board:
Asgarov S. (Azerbaijan), Alakbarov M. (Azerbaijan), Aliev Z. (Azerbaijan), Babayev N. (Uzbekistan), Chiladze G. (Georgia), Datskovsky I. (Israel), Garbuz I. (Moldova), Gleizer S. (Germany), Ershina A. (Kazakhstan), Kobzev D. (Switzerland), Kohl O. (Germany), Ktshanyan M. (Armenia), Lande D. (Ukraine), Ledvanov M. (Russia), Makats V. (Ukraine), Miletic L. (Serbia), Moskovkin V. (Ukraine), Murzagaliyeva A. (Kazakhstan), Novikov A. (Ukraine), Rahimov R. (Uzbekistan), Romanchuk A. (Ukraine), Shamshiev B. (Kyrgyzstan), Usheva M. (Bulgaria), Vasileva M. (Bulgar).
Phisics and Mathematics
Influence of radius of a
capillary on a vapor pressure. On basic data
[1, page 74] made tabular model, is given in table 1. In it massifs ![]() and
and ![]() basic
data for introduction to the program CurveExpert-1.40 [3] environment are noted.
basic
data for introduction to the program CurveExpert-1.40 [3] environment are noted.
|
Table 1 Compliance of radius of a capillary with pressure of water vapor
|
That says professor I.V. Krechetov [1, page 74] about the physical effect: «Pressure of water vapor in the capillary moistened by liquid over a concave surface of a meniscus is less, than over a flat water surface … From here it is visible that the vapor pressure considerably goes down only in ultramicroscopic capillaries …».
Note that
the data in table 1 are valid only for the temperature 20 °С. The
ratio between the radius of a capillary ![]() and relative
pressure decline of water vapor
and relative
pressure decline of water vapor ![]() is suitable
only for a raising explanation a tree on the considerable height of water
solution of nutrients from roots for foliage.
is suitable
only for a raising explanation a tree on the considerable height of water
solution of nutrients from roots for foliage.
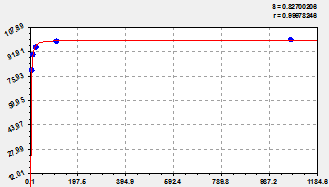
The determined model. On Weibull's distribution received (fig. 1) a formula
![]() . (1)
. (1)
|
|
|
Fig. 1. Schedules of a trend (at the left) and wave function of a wavelet signal (on the right)
In the right
top corner there are following designations: ![]() -
dispersion or sum of squares of deviations;
-
dispersion or sum of squares of deviations; ![]() -
correlation coefficient. The coefficient of correlation 0,9998 at the schedule
in figure 1 (at the left) according to table 2 belongs to the level «almost
unambiguous» model.
-
correlation coefficient. The coefficient of correlation 0,9998 at the schedule
in figure 1 (at the left) according to table 2 belongs to the level «almost
unambiguous» model.
Assessment of an error of a trend. For such assessment it is necessary to add the table of 1 basic data, at least, with three columns (tab. 2).
In this table
the following symbols are accepted: ![]() - the
actual experimental values of relative pressure of water vapor on basic data
[1, page 74], %;
- the
actual experimental values of relative pressure of water vapor on basic data
[1, page 74], %; ![]() -
settlement on model (1) value of an indicator, %;
-
settlement on model (1) value of an indicator, %; ![]() - absolute
error of model (remains) from a formula (1), %;
- absolute
error of model (remains) from a formula (1), %; ![]() - relative
error of model (1), %.
- relative
error of model (1), %.
The first four lines from table 2 belong to
nanocapillaries. The maximum relative error is on the second line and is equal ![]() .
.
Table 2. Assessment of an error of a trend of influence of radius of a capillary
on pressure
of water vapor at a temperature 20 0С
|
Capillary radius in wood
|
Relative pressure of water vapor |
Calculated values on model (1) |
Calculated values on model (2) |
||||
|
|
|
|
|
|
|
||
|
0.67 |
20.00 |
19.82 |
0.1803 |
0.90 |
20,00 |
0,0050 |
0,02 |
|
1.17 |
40.00 |
40.83 |
-0.8277 |
-2.07 |
40,01 |
-0,0135 |
-0,03 |
|
2.11 |
60.00 |
59.48 |
0.5169 |
0.86 |
59,99 |
0,0142 |
0,02 |
|
4.83 |
80.00 |
78.83 |
1.1698 |
1.46 |
80,01 |
-0,0146 |
-0,02 |
|
10.25 |
90.00 |
89.75 |
0.2510 |
0.28 |
89,99 |
0,0107 |
0,01 |
|
21.90 |
95.00 |
95.65 |
-0.6488 |
-0.68 |
95,00 |
0,0036 |
0,00 |
|
107.00 |
99.00 |
99.10 |
-0.1024 |
-0.10 |
99,00 |
-0,0028 |
0,00 |
|
1077.00 |
99.90 |
99.32 |
0.5848 |
0.59 |
99,90 |
-0,0028 |
0,00 |
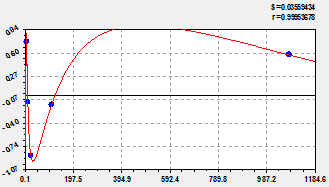
Trend building. Because of high precision we will add in model (5.1) only one wavelet. Wavelet is a signal (fig. 1, on the right) therefore for the analysis of the sucking force of live wood of growing trees further it is necessary to analyse the general equation with wave component. For the physical and mathematical analysis of heat treatment of wood cages it is necessary to make experiments at high temperatures.
Combining trend with wavelet. Each new member has to be attached to the previous design of a formula [3]. The effect of «shake-up» and «consolidation» by analogy to packing of different subjects in a box is thus gained.
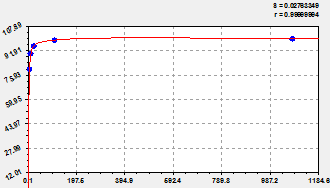
We will write down ready statistical model (fig. 2) in a look
![]()
![]() , (2)
, (2)
![]() ,
, ![]() ,
,
where ![]() -
amplitude (half) of fluctuation, %,
-
amplitude (half) of fluctuation, %, ![]() - a
half-cycle of fluctuation, nanometer.
- a
half-cycle of fluctuation, nanometer.
|
|
|
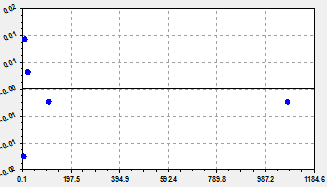
Fig. 2. Schedules of trinomial model (at the left) and the remains from it (on the right)
According to table 3 the maximum relative error of biotechnical regularity (2) is equal only 0,03%. Introduction of a wave component increased modeling accuracy in 2,07 / 0,03 = 69 times.
Conclusion. The remnants of figure 2 show that another possible wave component in nanoradii of capillary wood. But for further modeling it is necessary to make new experiments with much more exact measurements.
2. Mazurkin P. M. Dendrometry. Statistical studying of a tree: manual H. 1. Yoshkar-Ola: MarSTU, 2003. 308 pages.
3. Mazurkin P.M. Solution of the twenty third problem of Hilbert // Interdisciplinary research in the field of mathematical modeling and computer science. Proceedings of the 3-rd scientific and practical internet-conference. Ulyanovsk: SIMJET, 2014. P 269-277.
Mazurkin P.M. CAPILLARY PRESSURE IN WOOD
. International Journal Of Applied And Fundamental Research. – 2014. – № 2 –
URL: www.science-sd.com/457-24645 (26.04.2024).










 PDF
PDF