About Us
Executive Editor:Publishing house "Academy of Natural History"
Editorial Board:
Asgarov S. (Azerbaijan), Alakbarov M. (Azerbaijan), Aliev Z. (Azerbaijan), Babayev N. (Uzbekistan), Chiladze G. (Georgia), Datskovsky I. (Israel), Garbuz I. (Moldova), Gleizer S. (Germany), Ershina A. (Kazakhstan), Kobzev D. (Switzerland), Kohl O. (Germany), Ktshanyan M. (Armenia), Lande D. (Ukraine), Ledvanov M. (Russia), Makats V. (Ukraine), Miletic L. (Serbia), Moskovkin V. (Ukraine), Murzagaliyeva A. (Kazakhstan), Novikov A. (Ukraine), Rahimov R. (Uzbekistan), Romanchuk A. (Ukraine), Shamshiev B. (Kyrgyzstan), Usheva M. (Bulgaria), Vasileva M. (Bulgar).
Phisics and Mathematics
The structural features of worked out DKE are below given: DP 1(pic.1), BL (pic. 2). The prisms of type of DPPUD differ in that at normal incidence-fission of wave on the exit of prism is absent, but here maximal sensitiveness of "doubling" between о- and е-waves is achieved in relation to angle of incidence. The first variant of prism (DPPUD- 1) is presented on picture 1. The plane of optical axes is perpendicular an entrance and output to the verges of prism and parallel to the rib of prism.
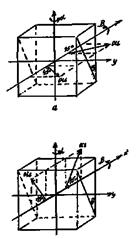
Fig.1. Construction of двупремляющих prisms of variable angle of doubling of type of DPPUD - 1(а) and DPPUD (b)
For a wave, falling inplane, containing optical axes, at any angles of incidence on the exit of DPPUD formed two о- and е- waves with the ortogonal state of пpolarization . Basic descriptions of DPPUD, measureable on experience, are doubling angle y between о- and е- rays on the exit of prism and angle of rejection of х came from the prism of е-ray from the plane of incidence. Calculation sizes y and х for DPPUD Д - 1 determined on formulas:
![]() ;
(1)
;
(1)
![]() , (2)
, (2)
where ![]() parameter of trifle ((δ
parameter of trifle ((δ![]() )/
)/![]() ;
;![]() ,
,![]() ,-main indexes of refraction of о- and е- waves;
,-main indexes of refraction of о- and е- waves; ![]() -deflectable angle of wedge of prism;
-deflectable angle of wedge of prism; ![]() azimuth angle, characterizing the turn of DPPUD about axis of
azimuth angle, characterizing the turn of DPPUD about axis of ![]() , the flat spreads along thatwave;
, the flat spreads along thatwave; ![]() angle of incidence on the entrance verge of prism,
equal to the angle of turn of DPPUD around axis x.
angle of incidence on the entrance verge of prism,
equal to the angle of turn of DPPUD around axis x.
The second variant of prism (DPPUD - 2) is presented on a picture 1,6. The plane of optical axes is perpendicular to an entrance and output to the verges, and also rib of prism. Here in this case we get:
![]() ; (3)
; (3)
![]() (4)
(4)
If a falling wave lies inplane optical axes at any angles of incidence, that takes place at (β=0, then breaking (up "doubling") on an exit takes place in plane of incidence, i.e. х2 = 0. If a wave falls in of, planes of optical axes, then breaking up is absent, as well as in case of DPPUD of Dependence of kind (1) - (4) are in a good consent with experimental facts and can be used for drafting of algorithms for COMPUTER in the systems of operation of a laser ray.
Properties of other element (BL) are described in works. Calculation of DKE of type of B.L., conducted on methodology, and explained on picture 2, c.
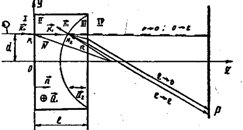
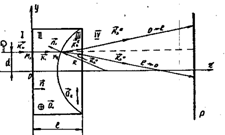
а) b)
c)
Fig. 2. Constructions of bifocal lenses of type
of BL- 1(а) and BL - 2(b) and chart of motion of rays in them(c)
Let in the circular polarized wave spreads in the direction of axis z. At such choice of the state
of polarization of falling wave "attachment" of vector of
polarization to the optical axis of crystal on the entrance of BL appears unimportant, that allows
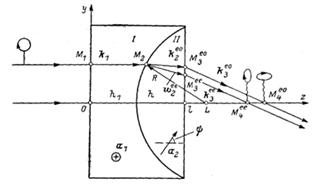
in future to unite the construction of theory for the lenses of type of BL- 1 and BL- 2. Let z=0 жэне z=ℓ are left and right to the verge of BL accordingly, and spherical border is set with
equation![]() where –distance from
the beginning of the system of coordinates
to the center of spherical surface of БЛ. Directions of optical axes in the
areas of I and II are set by the unit vectors of а1 -(1,0,0) and oh, = x2+у2+(z-δ)2=
R2, where δ - corner between BL and axis 2(fig. 2, c). Let (on the left verge of БЛ in the arbitrary
point of М1
the narrow parallel beam of light falls along an axis. The point of М1 has coordinates of dcosφ, dsinφ,0, where φ-angle between the axis of х and
radius-vector, conducted from beginning of coordinates z to the point M. Will suppose d<< R To,
where R -
radius of curvature of spherical border of division of BL., size (d/R)2 is scorned small. The
index of refraction for о-
wave
in the areas of I and II is identical and equal h0, and for a е- wave depends on
where –distance from
the beginning of the system of coordinates
to the center of spherical surface of БЛ. Directions of optical axes in the
areas of I and II are set by the unit vectors of а1 -(1,0,0) and oh, = x2+у2+(z-δ)2=
R2, where δ - corner between BL and axis 2(fig. 2, c). Let (on the left verge of БЛ in the arbitrary
point of М1
the narrow parallel beam of light falls along an axis. The point of М1 has coordinates of dcosφ, dsinφ,0, where φ-angle between the axis of х and
radius-vector, conducted from beginning of coordinates z to the point M. Will suppose d<< R To,
where R -
radius of curvature of spherical border of division of BL., size (d/R)2 is scorned small. The
index of refraction for о-
wave
in the areas of I and II is identical and equal h0, and for a е- wave depends on ![]() (i=1,2)- single wavy vector in the areas of I and II accordingly. In
area of K1, (1) coincides with direction of
light
ray.
There is mutual transformation of о- and е-волн on the spherical border of
division of БЛ. Wave
vector
(i=1,2)- single wavy vector in the areas of I and II accordingly. In
area of K1, (1) coincides with direction of
light
ray.
There is mutual transformation of о- and е-волн on the spherical border of
division of БЛ. Wave
vector
![]() in area of. II lies in plane, passing through an axis z and determined
by an
angle φ:
in area of. II lies in plane, passing through an axis z and determined
by an
angle φ:
![]() = (sinα2cosφ, sinα2sinφ, cosα2 ), where аг is an angle between
= (sinα2cosφ, sinα2sinφ, cosα2 ), where аг is an angle between ![]() and by an axis z. On a spherical border in general
case four waves must be considered and according to them four border conditions.
and by an axis z. On a spherical border in general
case four waves must be considered and according to them four border conditions.
Thus
the vector of ![]() and angle of α2 must add indexes(оо),(ое),(ео) ,
meaning: (оо) and
(ee) –keeping of type of polarization of wave;
(ое) and (ео) transformation of falling о- wave in the refracted е-wave and vice versa. Thus
and angle of α2 must add indexes(оо),(ое),(ео) ,
meaning: (оо) and
(ee) –keeping of type of polarization of wave;
(ое) and (ео) transformation of falling о- wave in the refracted е-wave and vice versa. Thus ![]() , and angle
, and angle ![]() can be found from the
law of refraction on a spherical surface:
can be found from the
law of refraction on a spherical surface:
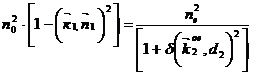
![]() (5)
(5)
where I![]() –single vector of normality. Intersection
–single vector of normality. Intersection
shining
with the spherical border of division has coordinates ![]() Putting in (5) values of vectors of
Putting in (5) values of vectors of ![]() and аг we will get the angles of
and аг we will get the angles of ![]() .
.
Wave vector of ray going out from BL, we will write down in a kind
![]() Obviously, that
Obviously, that ![]() and law of refraction (eo) of wave on the border of
and law of refraction (eo) of wave on the border of ![]() will
look like :
will
look like :
![]() (6)
(6)
where ![]() is a normal to the plane of z = е . From(6) will we get angles
is a normal to the plane of z = е . From(6) will we get angles ![]() .
.
For
being of е-ray in area of II it is required to
consider single
vector of
group speed on correlation of ![]() where μ1,μ2-coefficients. It is
necessary to angle
between in an anisotropic environment. It is possible to show that expression
for
where μ1,μ2-coefficients. It is
necessary to angle
between in an anisotropic environment. It is possible to show that expression
for ![]() describing the trajectory of е-ray in BL. looks like
describing the trajectory of е-ray in BL. looks like
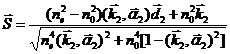 (7)
(7)
Case
of ![]() =0 suits to element of type of BL- 1 (рicture .2, а), and
=0 suits to element of type of BL- 1 (рicture .2, а), and ![]() - element of type BL- 2 (picture2, b). For the Icelandic spar n0>ne
and
- element of type BL- 2 (picture2, b). For the Icelandic spar n0>ne
and ![]() - we have
- we have ![]() . This means that о-ray going to the environment of II on leaving from BL- 2 walks away from the axis of Z; consequently, falling on BL - 2 a parallel bunch with this
polarization will be going
(picture.2, c) away. For(ео) - and(ee) - rays at
. This means that о-ray going to the environment of II on leaving from BL- 2 walks away from the axis of Z; consequently, falling on BL - 2 a parallel bunch with this
polarization will be going
(picture.2, c) away. For(ео) - and(ee) - rays at ![]() (in BL- 1) we have:
(in BL- 1) we have: ![]() and
and ![]()
Consequently,(ео)
- and(ее) -rays will cross the axis of z in two different points
corresponding to two focuses of ![]() . Thus, by means of BL- 1 the interesting case of SDM of
flat wave will be realized on two spherical waves with divided along an axis by
2 focuses into a size
. Thus, by means of BL- 1 the interesting case of SDM of
flat wave will be realized on two spherical waves with divided along an axis by
2 focuses into a size ![]() , depending on double-refracting properties of crystal
and thickness of h of plane-convex lens(picture 2, а). This property of BL- 1 can be used for a holographing
in polarized light
in
subsequent bunches with the managed intensity.
, depending on double-refracting properties of crystal
and thickness of h of plane-convex lens(picture 2, а). This property of BL- 1 can be used for a holographing
in polarized light
in
subsequent bunches with the managed intensity.
The calculations given above allowed in theory to predict, and in and experimentally to find out a spatial uninvariance( to irreversibility of passing of hertzian wave in relation to the axis of z) at the analysis of distribution of laser bunch through BL- 1 in directions( + Z) (- Z). The invariance of the polarization linear optical systems is unobvious. On the contrary, there is a necessity to examine the location of elements of optical chart in a polarization optics. By the methods of matrix optics easilyto prove, for example, that a result of passing of hertzian wave through a double-base polarizing element(polarization +λ/4 ) will be different on the state of polarization depending on that, from what part a wave falls on difficult element 2. DKE of type of BL- 1 demonstrates an unique case in this sense, when not only the state of polarization but also amount of waves on an exit and picture of interferencepolarized waves are different for opposite directions of distribution of light. At falling of flat wave on BL- 1 outside plane-convene lenses(picture 2, а) there is breaking up on four waves, from which waves that(оо) - and(ое) - I are: parallel to axes z, and(ee) and(ео) –waves are spherical waves with carrying (along an axis 2) focuses. In case of falling of flat wave on БЛ- 1 from the side of plane – convex lens(area of III on a fig. 2, а) on an exit formed one parallel and one converging astigmatic bunches with the ortogonal states of polarization. Unlike BL- 1 DKE of type of BL- 2 property of uninvariance does not possess. For BL- 2(fig. 2,b) forming is characteristic converging(ео) and going(ое) away waves as a result of transformation of е-waves in о- waves and vice versa.
BP(fig. 3, а) is two prisms from a
monaxonic crystal as equal-side trapezoids (prisms of Dove), agglutinate with large grounds by the layer of
glue, having an intermediate index of refraction of ![]() . Optical axes in making prisms located in a plane
perpendicular to the grounds of prisms parallel between then selves and form a angle 45° with the plane of gluing(fig.
3,6) together. the choice of orientation of optical axes is comfortable during
work with a laser source;-, to the vertical orientation of vector of Е of
laser radiation, (in parallel to the rib of falling normally on an entrance
verge A1 C1 a laser ray is divided into о- and
е-rays. thus о-ray tests a complete internal
reflection from the layer of glue. At falling on a verge A 1 B1 of
the second
laser ray (from an independent source or first ray) formed by an optical
division е-ray
passes
without
rejections
along an axis
Z
In subsequent о- and е-buckles there is interference on the exit
of BP.
. Optical axes in making prisms located in a plane
perpendicular to the grounds of prisms parallel between then selves and form a angle 45° with the plane of gluing(fig.
3,6) together. the choice of orientation of optical axes is comfortable during
work with a laser source;-, to the vertical orientation of vector of Е of
laser radiation, (in parallel to the rib of falling normally on an entrance
verge A1 C1 a laser ray is divided into о- and
е-rays. thus о-ray tests a complete internal
reflection from the layer of glue. At falling on a verge A 1 B1 of
the second
laser ray (from an independent source or first ray) formed by an optical
division е-ray
passes
without
rejections
along an axis
Z
In subsequent о- and е-buckles there is interference on the exit
of BP.
At the turn of BP on a small angle and about axis parallel to the rib of BP, о- and е-burkes on the exit of BP have relative movement 3. The condition of existence of interference(фотосмешения) is переналожение (cross-correlation) о- and е-burcles at bringing their vibrations over to one plane by means of analyzer.
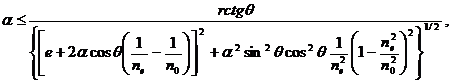 (8)
(8)
Thus top limit of measureable angles of turn where r-radius of the mixed up bunches; 2а, е, 0 are parameters of BP : length of the general founding, length of lateral side, corner at founding(fig. 3, в). For making from the Icelandic spar of BP with and=12mm, е=11mm, θ =65° from (8) we get α≤3º at the r of 3 mm.
2. Оsipov U.V., Optico-mechanic industry, 1973, № 5. p. 5; 1972, № 12, p. 1822.
З. Barsukov К. А., Оsipov U.V., Umbetov A.U. Distribution electromagnetic bullock two-component дlenses from monaxonic crystals. (Theory and experiment). 4260-83 of 01.08.83
Umbetov A.U. PARTICULARITIES DVUHKOMPONENTNYH KRISTALLOOPTICHESKIH SYSTEMS. International Journal Of Applied And Fundamental Research. – 2014. – № 2 –
URL: www.science-sd.com/457-24646 (15.02.2026).










 PDF
PDF