About Us
Executive Editor:Publishing house "Academy of Natural History"
Editorial Board:
Asgarov S. (Azerbaijan), Alakbarov M. (Azerbaijan), Aliev Z. (Azerbaijan), Babayev N. (Uzbekistan), Chiladze G. (Georgia), Datskovsky I. (Israel), Garbuz I. (Moldova), Gleizer S. (Germany), Ershina A. (Kazakhstan), Kobzev D. (Switzerland), Kohl O. (Germany), Ktshanyan M. (Armenia), Lande D. (Ukraine), Ledvanov M. (Russia), Makats V. (Ukraine), Miletic L. (Serbia), Moskovkin V. (Ukraine), Murzagaliyeva A. (Kazakhstan), Novikov A. (Ukraine), Rahimov R. (Uzbekistan), Romanchuk A. (Ukraine), Shamshiev B. (Kyrgyzstan), Usheva M. (Bulgaria), Vasileva M. (Bulgar).
Key words: convective superheater, boiler, non-stationary temperature conditions, internal microstresses, swell and break-up, crystal lattice, numerical modeling, analytical solution, approximate analytical solution, heat conductivity, double-sweep method, implicit scheme.
Introduction
It is known that there are superheater tubes as the main elements of boiler equipment more often damaged during the irrational operation. The overheating surfaces reliability depends on many different factors, such as: medium and metal temperature regime, pressure, dynamic heat and medium flow rate, heat emission, operating voltage values increase, steel chemical composition, insufficiently qualitative thermal treatment, local damages and the others. It should be noted that the joint action of several factors can be the superheater tube damages cause. The cause, considered in paper [1], can be an example. There are spontaneous high descent velocity sharp abrupt medium temperature and pressure changes at a direct flow boiler PK-33 two-stage superheater start initial moments for high heat emission and higher flow rates, as Petrosyan R. A. and others [1] note. So there are medium temperature and pressure values changes, resulting in the temper accumulation in different superheater elements and their further damage.
There were superheater tube straight elements swell and break-up even for permissible temperatures of operation, appropriate heat treatment, total permissible voltages and without damages in Russia and abroad, due to the authors’ grating [2,3], as to the studying overheating surfaces damage causes because of the austenitic chrome-nickel steels. At the same time there were the main causes of overheating surface wear such as: the tube material chemical composition change during the operation, the tube structure inhomogeneity, unfounded nickel overexpenditure, used for the operation reliability increase, the low deformation capacity, the unfavorable coil packet construction.
The change of metal thermal mechanical properties at the intracrystalline level is the general cause of superheater tube wear just-listed factors and the overheating surface damages fundamental investigation subject [4-8]. It’s noted in these papers that the I and II type microstresses, also phase changes, in turn resulting in different corrosion types, are the most essential causes of superheater tube damages. At the same time it should be noted, that the thermal stress changes mechanism under the temperature and pressure differences influence aren’t enough studied. It’s noted in many papers [9-12], that the I and II type internal microstresses and lattice linear thermal expansion anomalous changes are occurred at the temperature within the range of 650-720 °C. The phase changes, occurring at the intragrained level, are the cause of these effects, as to the author hypotheses. The thermal mechanical property changes investigation of tube metal is impossible without the knowledge about the temperature regime behavior relative to the radial and longitudinal coordinates in different superheater components.
The experimental method is taken as the main investigation way of the thermal mechanical process and temperature regime changes for the superheater operation non-stationary conditions [13-16]. Unfortunately, this method needs an appropriate equipment and a large financial expenditure. Also this equipment isn’t always available. As well, it should be noted, that an error-free information receipt, due to this method, on the temperature distributions in the tube cylindrical wall, varying with the time, is a difficult problem. Therefore the numerical modeling method is a more rational way to solve the similar problems. Nowdays, there are different mathematical models, describing laws of boiler heat processes and temperature change [17-20]. But the given results, in these works, haven’t enough information amounts as to the temperature regime behavior in the boiler superheater elements. There isn’t any information as to the obtained results’ validation method in these works too.
Taking into account the above-listed aspects, make following conclusion. One of the heat-and-power engineering actual problems is the superheater elements’ temperature regime investigation for the non-stationary conditions of operation with using numerical modeling methods.
The work aim is the numerical modeling of non-stationary convective superheater temperature regime.
Tasks
1. The physic-mathematical model statement for solving the non-stationary temperature regime of a superheater tube element;
2. The results validation, obtained during the physic-mathematical model numerical computation.
Physico-mathematical problem formulation
The round vertical boiler BKZ-75-39 superheater tube element with a clean surface is considered in this work, as an investigation object (Fig. 1). The one-dimensional non-stationary differential heat conduction equation with the starting and boundary conditions is used to determine the tube element cylindrical wall temperature regime and the third type boundary conditions are given on the left and right boundaries. The given data are taken from the steam generator certificate and shown at table 1. The following basic assumptions are made for the problem statement:
1. thermalphysic properties of smoke fumes, tube surface material, steam are constants;
2. the superheater tube element without internal defects in the crystal lattice is studied in this paper;
3. both smoke fumes and steam are considered to be an incompressible media. This tube element is washed by hydrodynamically and thermally stable flows.

Figure. 1. Diagram of the superheater tube elements
Table 1.
|
Symbol |
Characteristic |
Value |
|
r1 |
Cylindrical wall inner radius |
0,014 m |
|
r2 |
Cylindrical wall outer radius |
0,019 m |
|
Ср |
Cylindrical wall heat capacity (steel 20) |
504,8 J/(kg·˚С) |
|
ρ |
Cylindrical wall density (steel 20) |
7800 kg/m3 |
|
λ |
Cylindrical wall heat conductivity coefficient (steel 20) |
14,278 W/(m·˚С) |
|
α1 |
Heat-transfer coefficient from the cylindrical wall inner surface to the steam |
1741 W/(m2·˚С) |
|
α2 |
Heat-transfer coefficient from the smoke to the cylindrical wall outer surface |
60 W/(m2·˚С) |
|
t |
Heat time |
305 s |
|
Tc1, Tc2 |
Steam and smoke temperatures |
347, 823 ˚С |
|
Tn |
Starting temperature distribution in the wall |
340 ˚С |
The temperature distribution of the tube element cylindrical wall is determined by the following differential equation, given below.
Cp is steel heat capacity. The benchmark unit of heat capacity is joule per kilogram per Celsius degree. ρ is steel density, measured in kilograms per cubic meter. λ is steel heat conductivity coefficient, measured in watt per meter per Celsius degree. α1,α2 are heat-transfer coefficients from the inner surface to the steam and from the smoke to the outer surface respectively, measured in watt per square meter per Celsius degree. T1,T2 are steam and smoke temperatures on the left and right boundaries respectively, measured in Celsius degrees.
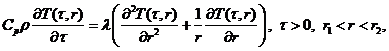
![]() (1)
(1)
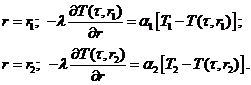
Investigation method
The above-mentioned mathematical model is determined as to the implicit scheme by double-sweep method [21, 22]. This numerical modeling method is more stable comparing with other methods, concerning implicit scheme. It is should be noted, that this method isn’t only stable solution method regard to rounding error, but also allows determining equations’ system, having few a unknown hundred. The computation simplicity, performing at the computer, is also this method advantage. The test problem solution is used to prove the implicit scheme applicability as to double-sweep method for solving similar problem, as formulated problem [23]. The analytical solution of concerning problem is known [23].
The differential equation approximate analytical solution (1) is made by following function:
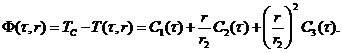 (2)
(2)
Turbo Pascal and MathCAD software are used to solve given problems.
Results and discussion
The following results were obtained during the physic-mathematical model solving.
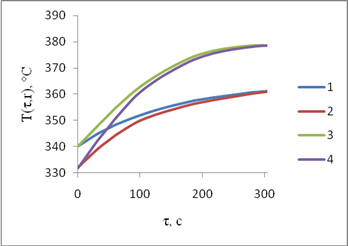
Fig.2. Outer and inner cylindrical wall surface temperatures respectively:
1, 3 – determined by analytical method; 2, 4 – determined by finite difference method
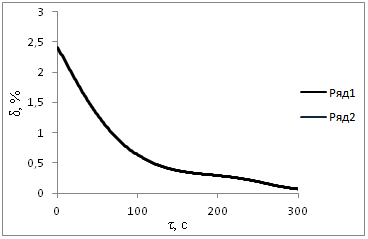
Fig.3.Error distribution:
1 – for inner cylindrical wall surface temperature; 2 – for outer cylindrical wall surface temperature
The outer and inner surface temperatures increases stable, apparently from obtained results. The process gains stationary character for a time epoch 305 s, due to constant thermal physical properties. The more stable curves, obtained by approximate analytical method, comparing with curves, obtained by finite difference method are easy to see. Results, got by approximate analytical method, are more accurate, than those, obtained by finite difference method, having some error, concern with computer calculation and approximation error, inaccuracy from these aspects could say. Error isn’t more 2 %, as the results confrontation, obtained by both methods, show for Fo numbers Fo>0,5 yet.
Conclusion
The formulated physic-mathematical model can be used to determine boiler superheater non-stationary temperature regime for Fo numbers Fo>0,5.
2 V.N. Gulyaev, N.V. Bulanov Heat and power engineering 11, 68–71 (1964).
3 V.A. Krijanovskiy Heat and power engineering 2, 6–12 (1964).
4 A.A. Zackirova, R.G. Zaripova, V.I. Semenov Mechanical engineering. Materials technology and metals thermal treatment 2, 123–130 (2008).
5 V.V. Mulchin, D.S. Lomonosov Mechanical engineering 4, 224–228 (2007).
6 O.Yu. Semenova Mechanical engineering and power engineering 1, 86–92 (2011).
7 M.M. Zackirinichnaya, I.R. Kuzeev, V.K. Berdin Oil and gas business 1, 207–214 (2006).
8 V.V. Artamonov, Control. Diagnostics 1, 8–11 (2010).
9 L.L. Lyubimova, A.A. Mackeev, A.A. Tashlickov Bulletin of the Tomsk polytechnic university 4, 26–31 (2012).
10 A.S. Zavorin, A.A. Mackeev, L.L. Lyubimova Bulletin of the Tomsk polytechnic university 5, 103–106 (2006).
11 A.S. Zavorin, L.L. Lyubimova, B.V. Lebedev Bulletin of the Tomsk polytechnic university 2, 78–83 (2003).
12 L.L. Lyubimova, A.A. Tashlickov, A.A. Mackeev. Bulletin of the Tomsk polytechnic university 6, 26–31 (2006).
13 V.V. Artamonov, Control. Diagnostics 10, 62–70 (2007).
14 V.A. Bogachev, O.Ye. Taran, Electric power stations 2, 21–24 (2002).
15 V.A. Bogachev Electric power stations 5, 20–23 (2009).
16 G.E. Verhovskiy, P.A. Lepaev Power engineering specialist 1, 25–28 (2010).
17 M.A. Kvetniy, V.B. Habenskiy, O.M. Baldina NPO CKTI (1973).
18 T.V. Urban, V.I. Melihov, O.I. Melihov Thermal power engineering 5, 70–74 (2002).
19 G.A. Pickina, O.M. Chickunova Thermal power engineering 8, 25–29 (2008).
20 V.V. Krashennickov Engineers and physicists journal 6, 1079–1082 (1970).
21 A.R.Dorohov, A.S. Zavorin, A.M. Kazanov, V.S. Loginov, Modelirovanie teplovidelyayushih sistem (Modelling of heat-generating complexes) (Publishing house of scientific technical literature, Tomsk, 2000).
22 Mitchell A. R. Griffiths D. F. The Finite Difference Method in Partial Differential Equations. Wiley, 1980. – 267 p.
23 A.V. Lickov Teoriya teploprovodnosti (Heat conductivity) (Government publishing house of technical theoretical literature, Moscow, 1967).
Loginov V.S., Parpiev А.T. CONVECTIVE SUPERHEATER TUBE TEMPERATURE REGIME. International Journal Of Applied And Fundamental Research. – 2014. – № 2 –
URL: www.science-sd.com/457-24697 (15.01.2026).











 PDF
PDF