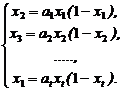About Us
Executive Editor:Publishing house "Academy of Natural History"
Editorial Board:
Asgarov S. (Azerbaijan), Alakbarov M. (Azerbaijan), Aliev Z. (Azerbaijan), Babayev N. (Uzbekistan), Chiladze G. (Georgia), Datskovsky I. (Israel), Garbuz I. (Moldova), Gleizer S. (Germany), Ershina A. (Kazakhstan), Kobzev D. (Switzerland), Kohl O. (Germany), Ktshanyan M. (Armenia), Lande D. (Ukraine), Ledvanov M. (Russia), Makats V. (Ukraine), Miletic L. (Serbia), Moskovkin V. (Ukraine), Murzagaliyeva A. (Kazakhstan), Novikov A. (Ukraine), Rahimov R. (Uzbekistan), Romanchuk A. (Ukraine), Shamshiev B. (Kyrgyzstan), Usheva M. (Bulgaria), Vasileva M. (Bulgar).
Keywords: cryptographic technique, chaotic behavior stabilization, encryption.
Introduction
The fact is known from the theory of dynamic system [1-4] that a sufficiently large family of chaotic dynamic systems features periodic disturbances that destabilize the cycle of a given period. The advanced cryptographic technique is based exactly on this fact; the data are encoded with this technique. The transmitted signal uses the disturbances ant the mapping type serves as the key to decoding the received message (in other words, the function setting the mapping).
Technique
The task is to develop the cryptographic technique based on stabilizing the dynamic system chaotic behavior; to explore all the necessary parameters of this cryptographic technique.
Main part
Let us consider the main postulates and the results obtained in the theory of dynamic systems regarding the chaotic behavior stabilization. Presently the most successful techniques of behavior (in other words, the behavior management) of dynamic systems are the technique of multiplicative effect with feedback and the technique without feedback [4, 5]. Let us assume that the system in question is determined with the common differential equations of the following type:
|
|
(1.1) |
where х = {x1, ..., xn} is the combination of dynamic variables, v = {v1, ..., vn} is some n-componential function and а is the governing parameter. The problem of controlling the system behavior (1.1) is to find which external disturbance G induces the phase flow Ft(x,G) when the disturbed dynamic system generates it at
|
|
(1.2) |
tends to the selected subset A(G) of its phase space.
The subset A(G) can be booth the attractor and the unstable set. In the latter case, the disturbances G modify the system (1.1) in such a way that thee phase trajectories approach the subset A(G) ad remain within its rather close vicinity UÉA(G) under the effect of G .
If the external disturbances are due to their multiplicative effect in respect too the dynamic variables хi, then they are said that their parametric (or multiplicative) control takes place because, as a rule, the parameters are multiplicatively incorporated into the dynamic system.
In this case, the control implies
such modification of the function v
in respect to (1.1) that the new system ![]() should have the required (selected in advance) behavior. Here
should have the required (selected in advance) behavior. Here ![]() and the parameter a1(t) are usually a Т-periodic
function.
and the parameter a1(t) are usually a Т-periodic
function.
When the parametric disturbances are
with the feedback, the current system state is taken into account:![]() .
The parameter а should change in a special manner rather than periodically.
.
The parameter а should change in a special manner rather than periodically.
The situation is rather frequent in applications when the multiplicative behavior of external disturbance in the system is feasible. Then the phase flow Ft(x,G) is factored into two components: the component corresponding to the non-disturbed phase flow Ft(x), and the component Ft(G) initiated exclusively by disturbances Ft(x,G) = Ft(x) + Ft(G). The additive disturbance occurs in this case, in other words, v'(x,a',t) = v(x,a) + g(t), where g(t) designates the external effect. Therefore, the dynamic system control implies the force component application to the vector function. Hence, this type of dynamic system behavior is termed forceful. In its turn, if the force control takes into account the feedback, then the function v is modified as v'i = vi (x,а) + gk(xi(t)), i = 1,2, ..., n, 1£k£n.
Due to a number of reasons, the
parametric dynamic stabilization technique has definite advantages over the
force one. First, the applications to chemical physical and other essential
systems often take into account the values, which are proportional to dynamic
variables хi. Such
systems have v(0,a1,...,am) = 0, while the hypersurfaces
хi are invariant
sets. It means that system (1.1) reflects real processes only at the simplex ![]() .
.
The external additive disturbance, in this vase, can lead to the phase trajectories leaving the set X intersecting the hypersurfaces хj =0. Since the force effect can cause degeneration of the system or its issue to the undesirable evolution mode. For instance, it means the extinction of a part of species in the biological systems. Meanwhile, the parametric effect implies the modification of the system resources, thus, it is finer than the force one. Second, the force disturbance is harder to implement. For instance, the force control of chemical systems implies the introduction (and elimination, respectively) of additional substances; the stabilization technique can be achieved in biological systems can be achieved by sterilizing a part of species or by introducing additional species into the colony. On the other had, in opposition to the parametric stabilization, the force technique, as a rule, leads to the desired result in almost all systems. It is because the natural behavior can be literally suppressed by any external force. The feedback introduction is a certain advantage because this control technique ensures the needed result in most cases: the saddle limit cycle selected beforehand is stabilized, thus, the system in question acquires the required motion mode. But this technique is effective only provided the imaging point is located close to the selected cycle. Otherwise, additional techniques of effect should be weighed. Meanwhile, the stabilization technique without feedback does not require any permanent computer (or any other) tracing of the system condition and it is less vulnerable to noise significantly simplifying its use in applications.
The main results obtained from the theory of dynamic systems and due to the stabilization of chaotic behavior exposed to external disturbances without feedback are the following [5, 6]. Assume the dynamic system (mapping) is specified as Ta: M®M,
|
Ta:xaf(x,a), |
(1.3) |
where aÎAÌ R and f = {f1, …, fn}, x = {x1, …, xn}. assume that this system has a chaotic behavior at definite parameter settings , in other words, there is a certain subset Аc, AcÌA , that the dynamics at aÎAc (1.3) (possible at some initial conditions) differ from the stationary, periodic or quasiperiodic dynamics. To stabilizeу the chaotic behavior, it is necessary to determine the disturbance G affective at the chaotic subset Аc, G :Аc® Аc,
|
G:aag(a),aÎAc, |
(1.4) |
so that the resulting disturbed dynamic system
|
|
(1.5) |
possesses stable cycles. During
periodic disturbance, the transformation G
setting the law of parameter modification is determined by the final set of
points {а1, a2, …, at}, being аi+1= g(ai),
i=1,2,…t-1, and а1 = g(at), а1, a2, …, atÎAc . in this case it is convenient to apply to each disturbance of the
period t of parameter the relevant vector ![]() from the space
from the space ![]() .
.
Then the subset ![]()
![]() can be considered as satisfying possible
effects of the period t, operating with Ac.
can be considered as satisfying possible
effects of the period t, operating with Ac.
works [6, 7] manifest that among the
sets ![]() making up the set Аc there
are such
making up the set Аc there
are such ![]() that mapping
(1.5) possesses stable cycles of limit periods, the period t of the obtained stable cycle being
multiple of the period of disturbance, t
= tk, where к = 1,2,.... This
situation turns out typical for a large class of chaotic mappings [8-10]. In
addition, the disturbances а1, a2, …, at can be found for
any family of unimodal and piece-linear mappings which have the disturbed
series with stable cycles and assigned periods.
that mapping
(1.5) possesses stable cycles of limit periods, the period t of the obtained stable cycle being
multiple of the period of disturbance, t
= tk, where к = 1,2,.... This
situation turns out typical for a large class of chaotic mappings [8-10]. In
addition, the disturbances а1, a2, …, at can be found for
any family of unimodal and piece-linear mappings which have the disturbed
series with stable cycles and assigned periods.
This result is based on the following
property: if the mapping Ta:xaf(x,a), xÎM, аÎA, has such a subset sÎM that a*ÎA is to be
found for any х1, х2Îs , for which f(x1,a*) = x2 and there is a critical
point хcÎs so that ![]() at
any аÎA, then for any x2, x3, ..., xtÎs, t = t, there are such х1 and а1, а2, ..., аt, that the cycle (x1,
x2, ..., xt) t = t, represents the
stable cycle of disturbed mapping Ta
at parametric disturbances а1, a2, …, at.
at
any аÎA, then for any x2, x3, ..., xtÎs, t = t, there are such х1 and а1, а2, ..., аt, that the cycle (x1,
x2, ..., xt) t = t, represents the
stable cycle of disturbed mapping Ta
at parametric disturbances а1, a2, …, at.
In the general case, the subset Ad corresponding to the stabilized behavior has a rather intricate structure [9, 10]. However, for the quadratic series
|
Ta:xaax(1-x), |
(1.6) |
with the periodic disturbance (а1, a2, …, at) the subset Ad corresponding to the cycles of period t = t turns out the whole region and it is fractioned into subregions that the disturbances within each subregion yields the stabilization cycle of a definite period. Exactly this result permits to use effectively this mapping to encode and dispatch the latent messages.
Let’s consider in detail the periodically (with the period t) disturbed series (1.6). it is convenient o rewrite it in the following way:
|
|
(1.7) |
If this mapping has the cycle of a period t = t, р = (x1, x2, ..., xt), then the points of this cycle satisfy the following system of equations
|
|
(1.8) |
To solve the inverse problem, in other words, to find the parameters at which the mapping (1.7) possesses a given cycle р = (x1, x2, ..., xt), it is necessary to express аi from the system (1.8):
|
|
(1.9) |
It is apparent that not at all хtÎ (0,1) there is aiÎ [0,4]. But,
providing this condition is satisfied at any cycle p = (x1,
x2, ..., xt), the parameters will be
found (а1, a2, …, at) at which disturbed mapping
(1.7) possesses the cycle р. At ![]() it
is stable.
it
is stable.
Taking to account equalities (1.9), this condition is written in the following way:
|
|
(1.10) |
Since at хс = 1/2 we have (l - 2хс)/(l - хс) = 0, then inequality (1.10) is always implementable. The series of values (x1, x2, ..., xt), at which aiÎ [0,4], inequality (1.10) is satisfied turning space Rt into the definite region with each point corresponding to the stable cycle of disturbed mapping. The transformation of this region with the system (1.9) yields the relevant region of parameters in the parametric space Rt.
The advanced cryptographic technique based on the stabilization of dynamic system chaotic behavior serves as the starting point for development of algorithms of cryptographic data transformation using the chaotic mapping.
Conclusions
The advanced cryptographic technique is based on the fact known from the theory of dynamic systems: there are periodic disturbances in sufficiently common series of chaotic dynamic systems leading to cycle stabilization within the set period. The data is encoded using these stabilized cycles. The disturbances serve as the transmitted signal with the mapping type serving as the key to decoding the received message.
The software is available at present implementing the cryptographic technique based on the stabilization of chaotic behavior of dynamic systems [11].
2. Loskutov, A.Ju., E.O. Petrenko, S.D. Rybalko and A.A. Churaev, 2004. Development of data encoding system implemented on the basis of stabilization cycles of maps of non-linear dynamic systems. Scientific session of MIFI-2004. 2.
3. Proc. Of the SPIE 1993 Annual Meeting «Chaos in Communication». San Diego California, 2038.
4. Dmitriev, A.S., 1991. А. data registration and identification in one-dimensional dynamic systems. Radioengineering and electronics, 5: 101-108.
5. Loskutov, A.Yu. and A.I. Shishmarev, 1994. Control of dynamical systems behavior by parametric disturbances and analytic approach. Chaos, 4 (2): 351-355.
6. Bainsby, M.A. and A.R. Oinarov, 2007. Determined chaos in economic system evolution. Institute of automation of NAN KR, Bishkek, Ilim, pp: 37-40.
7. Ten, T.L., M.A. Bainsby, and G.D. Coguy, 2012. Development of data protection system in distributed nets. Karaganda, KarGTU, pp: 193-197.
8. Alekseev, V.V. and A.Yu. Loskutov, 1987. Management of system with strange attractor using parametric effect. USSR Far East Acad. Scie., 293 (6): 1346-1348.
9. Marino, I.P., L. Lopez and M.A. Sanjuan, 2002. Channel coding in communications using chaos. Physics Letters A., 295, pp: 185-191.
10. Bainsby, M.A., T.L. Ten and G.D. Coguy, 2013. Management of determined chaos in distributed nets. Manual, Karaganda, KarGTU, pp:113-124.
Tatiana Ten, Galina Kogay CRYPTOGRAPHIC METHOD OF STABILIZING CHAOTIC METHOD OF DISTRIBUTED SYSTEMS. International Journal Of Applied And Fundamental Research. – 2014. – № 2 –
URL: www.science-sd.com/457-24698 (16.10.2025).











 PDF
PDF