About Us
Executive Editor:Publishing house "Academy of Natural History"
Editorial Board:
Asgarov S. (Azerbaijan), Alakbarov M. (Azerbaijan), Aliev Z. (Azerbaijan), Babayev N. (Uzbekistan), Chiladze G. (Georgia), Datskovsky I. (Israel), Garbuz I. (Moldova), Gleizer S. (Germany), Ershina A. (Kazakhstan), Kobzev D. (Switzerland), Kohl O. (Germany), Ktshanyan M. (Armenia), Lande D. (Ukraine), Ledvanov M. (Russia), Makats V. (Ukraine), Miletic L. (Serbia), Moskovkin V. (Ukraine), Murzagaliyeva A. (Kazakhstan), Novikov A. (Ukraine), Rahimov R. (Uzbekistan), Romanchuk A. (Ukraine), Shamshiev B. (Kyrgyzstan), Usheva M. (Bulgaria), Vasileva M. (Bulgar).
Engineering
In this paper, an express method is proposed for determining the slope of the left branch of the fatigue curve by using interpolation functions to obtain experimental dependences on the frequency of loading cycles. These relationships allow us to determine the value of the slope angle of the fatigue curve at any frequency of cyclic loading within the experimental data that are available. Thus, there is no need to carry out an experiment if, for a given loading frequency, it does not exist, but the desired value of the fatigue resistance index at the required loading frequency falls within the limits for which the experimental data are available. The tests were subjected to steel grade 40X for fatigue at three values of the cyclic loading frequency (ω) [1-2]. The data obtained in the figure show an increase in the cyclic strength with increasing (ω) (Fig. 1). It should be noted that at ω = 2 Hz in the region of small N, it has a higher cyclic strength than at ω = 2.7 Hz; however, due to a steeper slope, the curve drops lower and on the basis of N = 106 cycles a noticeable The difference in the values of limited fatigue cycles.
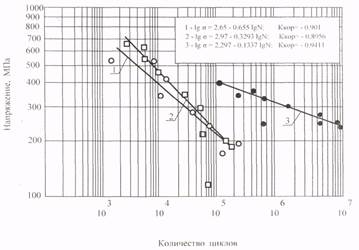
Fig. 1. The curves of fatigue of steel 40X at 20°C, 1,2,3-frequency loading 2; 2,7; 100 Hz. The bending deformation of the rotating sample
We apply interpolation functions to obtain experimental dependences of the material fatigue resistance parameter on the frequency of loading cycles, that is, tg αw = f (ω). These relationships allow us to determine the value of tgαw at any frequency of the loading cycles within the experimental data that are available. In other words, there is no need to conduct an experiment if, for a given frequency of loading cycles, it is not present, but the value of ω falls within the limits of the values over which the experimental data are available. The mathematical expression for this purpose looks like this:
tgαw=G0 + G1 (ω−ω0) + G2 (ω−ω0) ( ω−ω1), (1)
continue to expand it:
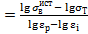 ;
; 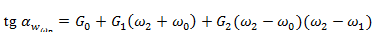 (2)
(2)
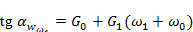 ; (3)
; (3)
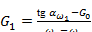 ; (4)
; (4)
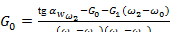 ; (5)
; (5)
Taking the experimental data for cadmium in Fig. 1 and assigning the relevant values ωi and 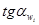 we have:
we have:
ω0 = 2; ω1 = 2.7; ω2 = 100 Гц;
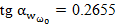 ;
;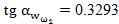 ;
; 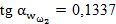
The calculation will get the coefficients of the expression:
G0 = 0.2655; G1 = 9.5695·10-2; G2= − 9.9699·10-4.
Substituting the numerical values into the expression (1) we get:
tgαw(ω)|Cт.40Х = 6.889·10-2 + 10.035·10-2 ω – 9.9699·10-4 ω2.
2. Mylnikov V. V., Shetulov D. I., Chernyshov E. A. On evaluation of durability criteria in carbon steels // Metals Technology. 2010. No. 2. p. 19.
Shetulov D.I., Mylnikov V.V., Kondrashkin O.B., Pronin A.I., Chernyshov E.A. APPLICATION OF INTERPOLATION FUNCTIONS IN THE EXPRESS EVALUATION OF PARAMETERS OF FATIGUE RESISTANCE. International Journal Of Applied And Fundamental Research. – 2017. – № 3 –
URL: www.science-sd.com/471-25288 (19.01.2026).











 PDF
PDF