Discusses the use of vertical rectangular cavities to control the busy state during explosive and non-stationary seismic wave influences. For the solution of two-dimensional non-stationary dynamic problem of elasticity theory with initial and boundary conditions we use the method of finite elements in displacements. In works [1–5] is some information on the practical implementation of numerical modeling of non-stationary of stress waves in complex deformable objects using numerical method, algorithm and software.

The calculations were conducted with the following initial data: 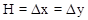; 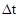= 1,393×10^-6 с; E = 3,15×10 ⁴ МПа; 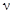= 0,2; 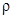= 0,255×10⁴ кг/м3; 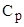= 3587 м/с; 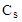= 2269 м/с. Solve the system of equations of 59048 unknown.

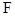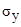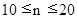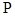Consider the task focused on the impact of the blast wave on the free surface of an elastic half-plane with the cavity (ratio of width to height of one to twelve) (fig. 1). At the point perpendicular to the free surface applied concentrated normal stress (fig. 1), which, when changes linearly from to , and when from to (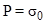, 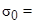- 0,1 МПа). The boundary conditions for the contour 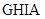in 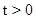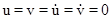. The reflected waves from the contour 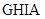do not reach to the point when 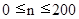. Contour free of loads, besides the point , where is applied a concentrated elastic normal stress 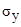. The results of calculations for grid voltages 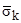(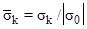) in time 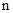received at the point 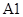(fig. 2), located on the free surface of an elastic half-plane: 1 – in the problem without cavity; 2 – in the problem with the cavity (the ratio of width to height of one to twelve).

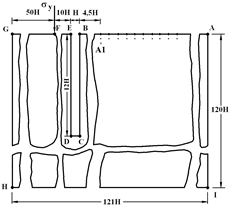
Fig. 1. The problem statement focused on the impact of the blast wave on the free surface of an elastic half-plane with the cavity (ratio of width to height of one to twelve)

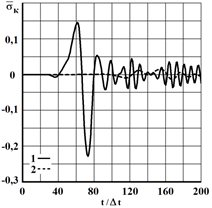
Fig. 2. The change of elastic contour stress 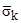in time 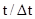at the point 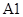: 1 – in the problem without cavity; 2 – in the problem with the cavity (ratio of width to height of one to twelve)

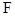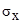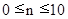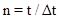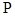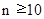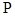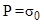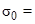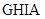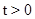
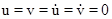Consider the problem of the influence of flat longitudinal seismic waves parallel free surface elastic half-plane with the cavity (ratio of width to height of one to twelve) (fig. 3). From the point parallel to the free surface applied normal stress , which, when () varies linearly from to , and when same (,0,1 МПа). The boundary conditions for the contour in . The reflected waves from the contour do not reach to the point when 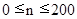. Contour 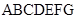free from loading, besides the point 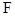. The results of calculations for grid voltages 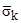(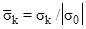) in time 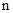received at the point 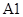(fig. 4), located on the free surface of an elastic half-plane.

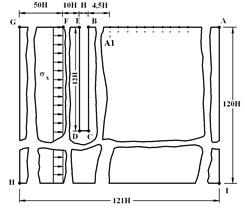
Fig. 3. Statement of the problem on impact of a flat longitudinal seismic waves on an elastic half-plane with the cavity (ratio of width to height of one to twelve)

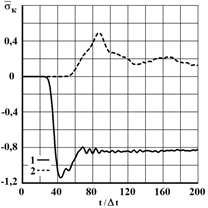
Fig. 4. The change of elastic contour stress 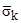in time 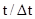at the point 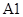: 1 – in the problem without cavity; 2 – in the problem with the cavity (ratio of width to height of one to twelve)

2. Musayev V.K. Estimation of accuracy of the results of numerical simulation of unsteady wave of the stress in deformable objects of complex shape // International Journal for Computational Civil and Structural Engineering. – 2015. – Volume 11, Issue 1. – P. 135–146.

3. Musayev V.K. On the mathematical modeling of nonstationary elastic waves stresses in corroborated by the round hole // International Journal for Computational Civil and Structural Engineering. – 2015. – Volume 11, Issue 1. – P. 147–156.

4. Musayev V.K. Modeling of non-stationary of stress waves in the shell with an elastic half-plane under the influence of air shock waves // International Journal Of Applied And Fundamental Research. – 2015. – № 2. – URL: www.science-sd.com/461-24853.

5. Musayev V.K. On the numerical simulation of elastic stress waves in the problem of Lemba for vertical centering exposure in the form of delta functions and Heaviside functions // International Journal Of Applied And Fundamental Research. – 2016. – № 2. – URL: www.science-sd.com/464-25144.