As is known [1-2], the process of fatigue destruction of metals and alloys occurs by the gradual development and accumulation of damages, first submicroscopic, then microscopic, followed by a transition to macroscopic discontinuities - the formation of fatigue cracks.

The influence of the cyclic loading conditions is taken into account by the stress level under various stress conditions (bending with rotation, tension-compression, torsion, etc.), loading frequency [3-5] and temperature.

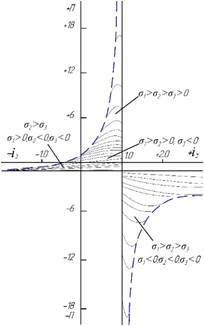
Theoretically, the possible values of the stress state index П are obtained from the analysis of the expression 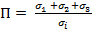under the condition that σ1 > σ2 > σ3 ≠ 0. They are shown in Fig. 1, a, in the coordinate system П=φ (i1, i2, i3), где i1 = σ1 / σ1 = 1.0; i2 = σ2 / σ1; i3 = σ1 / σ1 (Figure 2, b). The graphs of a line of the same concentration П (Fig. 2a) for П > 2 will be an ellipse, for П = 2 – a parabola and for П < 2 – a hyperbola. The scope of the function is found from the inequalities 1 ≥ i2 ≥ i3 и 1 ≤ i2≤ i3. The region defined by the first inequality (Fig. 2, a) is denoted by the letter A, the second inequality by B. The function Π will be positive in the region B only in the triangle designated by the hatching, bounded by straight lines: i3 = i2; i2 = 1,0 и i2 + i3 = 1,0. In all other cases of the region B, and also in the whole region A, the quantity Π is negative.

Values of П in the interval from - 18 до + 18, covering practical areas of stress states of mechanical tests are shown in Fig. 2, b (for σ1 > σ2 > σ3 ≠ 0). They can be attributed to any stage of the behavior of a deformable solid, including the elastic, plastic regions and the moment of its destruction.

If we consider the essence of cyclic loading and fracture, in fact it reduces to a competition between the loading rates (εн) and the relaxation rate of internal stresses (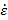рел=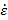р) [6], consisting in the accumulation of damages and actually being the rate of fall of the fracture resistance (σк) of the material i.e. 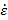р To assess the ultimate deformation of metal alloys and the resistance to cyclic deformation of polycrystals depending on the factors of their state: the ratio of the density in the initial and final states, the structural-energy state (the consistency of hardness and the yield point), the stress-strain state and the ratio of internal stress relaxation rates and loading rates, the following equations are proposed:

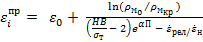(1);

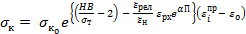(2),

where 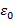– is the elastic deformation; 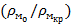– the initial density of the metal; HB – hardness of the material (alloy) in a given thermomechanical state; σт – is the yield point (elasticity) of the material base at which shear under cyclic loading is possible; П – is the stress state index, varying from - ∞ (under compression) to + ∞ (under tension); α – is a coefficient that takes into account the influence of the Lode coefficients-the type of strains and stresses.

 a)

 b)

Fig. 1. The theoretical value of the stress state index Π, calculated from the expression П = ± (σ1 + σ2 + σ3) / σi: a - depending on the dimensionless quantities i1 = σ1 / σ1 = 1.0; i2 = σ2 / σ1; i3 = σ1 / σ1 (real ranges of П are denoted by solid lines); b - the same, but in another coordinate system, in the range of values of П from -18 to +18

2. Mylnikov V.V., Romanov A.D., Shetulov D.I., Khlybov A.A. Effect of the aging temperature of steel on the parameters of fatigue resistance and microstrain // Metal Science and Heat Treatment. 2016. – р. 1-3.

3. Mylnikov V.V., Shetulov D.I., Chernyshov E.A. Variation in faktors of fatigue resistance for som pure metals as a function of the freguensy of loading sycles // Russ. J. Non-Ferr. Met. – 2010. Vol. 51, No. 3. – р.237–242.

4. Mylnikov V.V., Shetulov D.I., Chernyshov E.A. Investigation into the Surface Damage of Pure Metals Allowing for the Cyclic Loading Frequency // Russ. J. Non-Ferr. Met. – 2013. Vol. 54, No. 3. – р.229–233.

5. Mylnikov V.V., Shetulov D.I., Chernyshov E.A. Speed Effect upon Varying the Cyclic Loading Frequency for Certain Pure Metals // Russ. J. Non-Ferr. Met. 2015. Vol. 56. No. 6. pp. 627–632.

6. Skudnov V.A. Limiting plastic deformation of metals. - Moscow: Metallurgy, 1989. - 176 p.