A model of the strategy for optimizing scientific creativity, developed on the basis of the theory of information virtualization, is proposed. The development of the proposed approach to optimizing scientific creativity will improve the quality and effectiveness of scientific research in solving research problems in higher education institutions.

Key words: scientific creativity, information virtualization theory, discrete ensemble, joint ensemble, entropy.

Introduction.

The development of science in the framework of scientific and technological progress of recent times occurs in the absence of a clear scientific and philosophical understanding of the very processes of creativity and cognition. The result is a dangerously low efficiency of using scientific potential in practically all scientific fields. One of the ways to solve this problem is the development of a model of the strategy for optimizing scientific creativity from the standpoint of the theory of information virtualization [1,2]

Material and methods.

From the standpoint of the theory of information virtualization, the process of scientific creativity can be represented as an injective mapping of the form

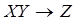(1)

where XY–is the joint ensemble combining the input data X and the discrete ensemble of methods (algorithms) of the creative search Y; Z–is a discrete ensemble of creative search results.

Within the framework of the accepted view (1) it can be considered that the process of scientific creativity is characterized by the joint entropy H [X Y Z]:

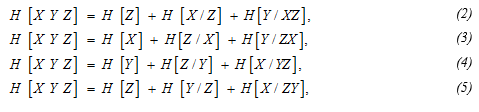
Equating the right-hand sides of expressions (2) and (3), and also the right-hand sides of (4) and (5), one can obtain a system of equations of the form:

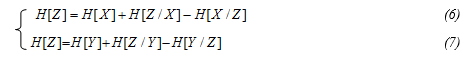
The resulting system of equations can be considered as a model of the strategy of scientific creativity.

Results and discussion.

The main condition for the optimality of this model is equality

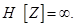(8)

In view of the discreteness of the ensembles X, Y and Z, this condition can be considered only as a guide for optimizing the strategy of scientific creativity. Therefore, in this case, as an achievable optimization condition, only the approximation of equality (8) can be considered:

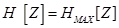(9)

In contrast to condition (8), which, in combination with the system of equations (6) and (7), determines the optimal model of scientific creativity, equality (9) in combination with the same system of equations allows us to obtain only quasioptimal ones, that is, approximations to optimal model. And the degree of this approximation will be the higher the value of the value will be..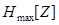

The optimal creative solution is always characterized by high unpredictability of the way that allows it to be obtained. High unpredictability of the solution method requires an increase in the entropy H[Y]. This can be achieved by increasing H[X] and H[Y/X]. The conditional entropy H[Y/X] characterizes the uncertainty of the choice of the solution method after setting the problem. In practice, an increase in H [Y/X] means the removal of restrictions (including those theoretically proven at the moment) in determining the method of solution for a given formulation of the problem.

A characteristic feature of optimality is an increase in the maximum entropy of ensembles, to which already known methods of solutions refer. Proceeding from the well-known expression for the maximum entropy

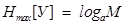(10)

such an increase is possible by increasing the number M of the components of the sample space of the ensemble Y. In practice, this means a broad inclusion in the sample space of methods from other scientific fields and directions. This is what A. Einstein did in his time, using the approach used to create the general theory of relativity, with the help of which Maxwell's theory, approved at that time, was obtained.

Conclusions.

The development of the proposed approach to optimizing scientific creativity will undoubtedly improve the quality and effectiveness of scientific research. However, while its use should be treated with a certain degree of caution. This is due to the fact that it is justified only with the help of information theory without taking into account spiritual, psychological, etc. factors.

2. Kotenko V.V, Kotenko S.V. Identification analysis of cryptographic algorithms from the point of virtualization of identifiers / Izvestiya SFU. Technical science. 2015. №. 8 (169). 32-46 p.