One of the methods of detection hypophysis volume that is used in roentgen and magnetic resonance tomography is based on measurement of three parameters: length of hypophysis, or its anteroposterior size, its width (lateral size) and height - craniocaudal size. It´s known in medical practice as Di Chiro-Nelson method [1-4], that can be expressed with the next formula:

where V - the volume of hypophysis (mm3); H - the height of hypophysis or craniocaudal size (mm); W - width or lateral size (mm); L - the length of hypophysis or anteroposterior size (mm).

This method of detection hypophysis volume is used successfully by clinicians and specialists in radiodiagnostics up to present day in spite of its antiquity [1].

Rough estimate of hypophysis volume is the principal disadvantage of this method, since it is presumed initially that hypophysis shape is similar to this of haricot or looks like cylinder with roundish edges.

But as practice shows, the size, shape and location of sella Turcica and hypophysis may vary significantly. Anatomical and age-specific features of sella Turcica texture, physiological and pathological processes cause additional complications in estimation of hypophysis structure [5-7]. Due to this fact the volume of hypophysis may change and physiological error appears in calculations that can make up from 30 to 50 % according to formula Di Chiro-Nelson. Especially frequently this estimation error emerges in cases of wide or narrow sella Turcica and modified shapes of hypophysis (see scheme 1). This error appears in the presence of slanting hypophysis position, when one or both of its edges are raised, or in cases of hypophysis adenoma with differently directed scalloped growth. The hypophysis volume calculated from this formula will be strongly determined by sites of measurement of height, width and length in such situations.

Reasoning from stated facts, the present work was undertaken to improve the precision of hypophysis volume calculation according to sagittal section parameters obtained by low field magnetic resonance tomography.

The posed problem could be decided by technical solution that is based on sagittal slices square, distantional factor and number of slices trough the hypophysis.

Methods

The research was performed on the lowfieled magnetic resonance imaging tomograph «Magnetom-Open» (Siemens) with magnetic field tensity 0,2 Tl with the use of standard T1 weighted images.

The authors method is based on receiving hypophysis image in saggital sections according to T1 with parameters TR (time repetition) = 340, TE (Time echo) = 26, number of slices (No. Slices) = 7, Slices Thickness = 3 mm; Field-of view - 230, matrix - 192´256, No. Acquisition = 6.

After getting image, estimation of square of each sagittal section trough the hypophysis is performed according to standard protocol. Special program can be used for this purpose, for example - region of interest (ROI), which is integrated in the most of tomographs and serve for calculation of ischemic or focal damage square. Slices squares are outlined with the help of program region of interest.

Each slice passing through the hypophysis in sagittal section carry established by operator information about itself, and there are two the most important physical parameters essential for hypophysis volume calculation in this case. The first is slices thickness and the second is distantional factor that reflect distance between slices. Both these parameters (slice thickness and distantional factor) can be established and changed by researcher. In this case slices a 3 mm thick are enough to receive detailed hypophysis characteristic when using standard protocol destined for hypophysis structure and size estimation. Distance between slices will show 0,3 mm in the presence of slice a 3 mm thick and distantional factor equal 0,1.

Hypophysis volume can be expressed by formula based on layer thickness, i.e. number of slices through hypophysis, their square and distantional factor that reflects the distance between slices. Thus our formula is based on the sum of slices volumes:

where V _H- hypophysis volume; S1 (h1 + d) - the first sagittal layer volume (V1); S2 (h2 + d) - the second sagittal layer volume (V ); S3 (h3 + d) - the third sagittal layer volume (V3 ), etc.

h + d - sagittal layer thickness composed of slice thickness (in our case it is equal 3 mm) and distantional factor (it is equal 0,3 mm for the present thickness). It is equal 3,3 mm in our research.

While multiplying together section thickness and its square we receive the volume of one section, and while summarizing volumes of individual sections through hypophysis we receive hypophysis volume, i.e.

where V _H - hypophysis  volume; V1+ V2 + V3 + ...+ Vn - volumes of individual sections taking into account correction of distantional factor. 

Formula for hypophysis volume estimation could be received after the conversion:  

In our case:

Sagittal section is received here due to the use of the program region of interest and outline of interesting material manually. Programs of outline of regions of interest are attached usually to each computer tomograph and are used for other purposes.

Thus it is necessary to set parameters of slice thickness (3 mm), distantional factor (0,1) for determining precise hypophysis volume, to lay plane of slices (package of slices) on the present scout trough the frontal plane. After receiving each slice square we can calculate the volume of hypophysis taking into account distantional factor and slice thickness.

Frequently occurring hypophysis shapes in frontal plane are present on the scheme 1.

Scheme 1. The most frequently occurring hypophysis shapes. The notations: 1, 2 - frequently occurring hypophysis normal shapes; 3, 4, 5 - pubertal hypophysis shapes; 6, 7, 8, 9, 10, 11 - the hypophysis in wide sella Turcica; 12 - the hypophysis with scalloped edges; 13, 14 - rounded hypophysis and hypophysis in narrow sella Turcica; 15, 16 - hypophysis shapes in empty sella Turcica

Calculations according to Di Chiro-Nelson formula can give a mistake, which can average from 30 to 50 % in these cases. The diversity of hypophysis shapes are usually determined by sella Turcica shape, which depends on forming and development of cranial bones.

Different hypophysis shapes are present further

The order of operations, which are necessary to receive hypophysis volume, is:

1. Sagittal slices with previously characterized parameters of T1 weighted image protocol are laid on the present scout in the frontal plane. The stacking order of slices for receiving images in the sagittal plane is shown on fig. 1. According to protocol seven slices are laid on the frontal plane.

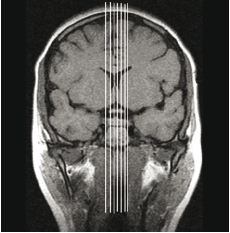
Fig. 1. Superposition of the slice plane on the scout through the frontal plane

2. Visible hypophysis region is outline on the received sagittal sections, using region of interest program.

3. Hypophysis volume can be received after inserting squares values in the formula (3).

Results and Discussions

Using this method pituitary gland volume was estimated in two groups of patients - with roundish shaped hypophysis (n = 15, women 20-30 years old), and empty sella Turcica and flat shaped hypophysis (n = 18, women 40-60 years old). In both groups the volume has been calculated according to Di Chiro-Nelson formula and formula suggested by authors´. The volume of pituitary gland that was estimated according to Di Chiro-Nelson formula in the group of patients with roundish shaped hypophysis was 305,8 ± 86 mm3, the volume in the group of patients with flat hypophysis shape was 233 ± 81 mm3, and were respectively equal 562 ± 107 mm3 and 433 ± 106 mm3 according to authors´ formula (Table 1).

Received results can be visually presented by bar graphs and range diagram (Diagram 1).

Data analysis was carried out with the help of program package Statistica 6.0. Comparison of these samples was performed with the help of nonparametric Wilcocxon test. The usage of parametric tests is uncertain in this case because amount of sampling doesn´t permit to suggest normal distribution of received variates with the high significance.

Accurate estimate for comparison of two groups of variables is given by Wilcocxon matched pair test. After its application to each group the hypothesis of significant difference of variates was confirmed, significance level has being very high and equal α > 99,9 % or p < 0,001 in both groups. Consequently these two methods of measurement hypophysis volume differ significantly.

Box &Whisker Plot or range diagram was constructed for visualization (Diagram 1, Diagram 2). The volume (mm3) is marked on axis of ordinates.

The results of hypophysis volume calculations in two groups

Table 1

Standard deviate (SD), mean and standard error (SE) are presented on diagrams in both groups.

Hypophysis volume received by authors´ formula 45 % higher then received by Di Chiro - Nelson formula.

Сonclusion

Due to the described information hypophysis volume estimation according to sagittal sections allows to receive more veritable parameters of hypophysis size, detection of volumes of hypophysis with complicated shape and in cases of complicated sella Turcica that usually cause error are described as the most accurate. At the same time Di Chiro - Nelson formula allows to detect volume correctly only in case of cylindrical hypophysis shape. Its usage in the presence of atypical sella Turcica configuration and other peculiarities described above is difficult and may lead to approximate volume detection. Our research had permitted to determine new hypophysis volume values, in the group of roundish hypophysis shape the volume

Diagram 1. Correlation of ranges of values, means and standard errors in the group of patients with roundish hypophysis shape according to Di Chiro - Nelson formula (on the left) and according to the authors formula (on the right)

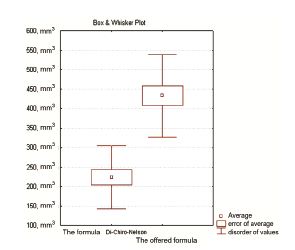
Diagram 2. Correlation of ranges of values, means and standard errors in the group of patients with flat hypophysis shape and empty sella Turcica syndrome according to Di Chiro - Nelson formula (on the left) and according to the authors formula (on the right)

of pituitary gland was 562 ± 107 mm3, in the group of flat shape (empty sella Turcica syndrome) it was 433 ± 106 mm3 in particular.

The authors´ method doesn´t minimize the importance of hypophysis volume estimation according to Di Chiro - Nelson formula yet, which is the most simple in calculations. But in our opinion it is appropriate to introduce correction factor in this formula, while calculation of volume of hypophysis with complicated shape, correction factor is equal 1,33 according to our data. Then it is necessary to add extra 1/3 of obtained volume to the hypophysis volume estimated by Di Chiro - Nelson formula. Received values will reflect desired hypophysis volume to a greater extent in the view of complicated sella Turcica configuration.

References

1. Di Chiro G., Nelson K.B. The volume of the sella turcica // Am J Radiol. - 1962. - V. 87. - P. 989-1008.
2. Lundin P., Pedersen F. Volume of pituitary macroadenomas: assessment by MRI // Journal of Computer-Assisted Tomography. - 1992. - V. 16. - P. 518-528.
3. Zielenski G., Podgorski J., Koziarski A. et al. Preoperative administration of a slow realizing somatostatin analog (SR-lanreotide, BIM 23014) in patients with acromegaly in the course of GH-realising adenoma // Neurol Neurohir Pol. - 2001. - V. 35. - P. 423-37.
4. Belov S.A., Ahadov T.A., Kravtsov A.K. Materials of the Researchand-Practical Conference. Modern Opportunities of the Magnetic Resonance Tomography. - M., 1998. P. 29-33.
5. Dedov I.I., Belenkov J.N., Belichenko O.I., Melnichenko G.A. Magnetic Resonance Tomography in the Hypothalamic-Pituitary and Adrenal Gland Diseases Diagnostics. - M.: Medicine, 1997. - P. 160.
6. Konovalov A.N., Kornienko V.N., Pronin I.N. Magnetic Resonance Tomography in Neurosurgery. - M.: Vidar, 1997. - P. 171.
7. Elster A. D. Moder imaging of the pituitary // Radiol. - 1993. - V 187. - P. 1-14.