Let the stationary process be presented as a linear operator equation

I rotT + B grads = 0, div T = 0, (1)

where components u, v, w of the vector T, and scalar function s are dependent variables of arguments x, y, z, I and B are given matrixes

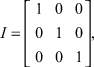
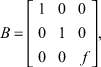
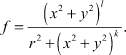
With positive values of parameters l, k, r [1-3, 6].

As we approach the origin of the excitation, the studied fixed process starts to alter its structure - elliptic system (1) parabolically degenerates in the multiplicity x2 + y2 = 0, and for it common classic setting of problems of modern mathematical physics become incorrect [7].

The first boundary problem.

Let us study the behavior of the system (1)

u_x + v_y + w_z = 0, w_z - u_z - s_y = 0,

v_z - u_y + f(x, y)s_z = 0, s_x - v_z + w_y = 0.

Near the degeneration line x = y = 0 that is contained in cylinder

D = {(x, y):x² + y² < R², 0 < z < z₀}

with side surface Г, upper Г₁ and bottom Г₀ bases. Let us define D₀ as a part of axis OZ, that lies in .

Problem 1.

Find all conditions of existence and uniqueness in area D of the limited on the multiplicity of degeneration D₀ solution of the system (1).

While l > 0, k = r = 0, conditions of the correctness of the problem are defined in [4].

In the presented work under terms

    (2)

where         

The following is proved.

Theorem 1. While l = k = 1 и r = R in classes of the function smoothness

exists a limited near the degeneration axis solution (u, v, w, s) of the problem (1)-(2), where u and v are defined with a precision up to random constant summand, and a, w, and s - in a single way.

Through a reduction of the results of differentiation and integration of the equations (1) according to the corresponding variables we obtain a system:

?w = 0, s_xx + s_yy + f(x, y) s_zz = 0,

Functions J(y, z) and Q(y, z) are defined precisely up to the random constant summand from the system

The main point in the proof of the theorem is:

Lemma 1. Boundary problem

 (3)

   (4)

Has a unique solution in the cylinder D, that is limited while (x² + y²) → 0.

The proof is carried out according to the classic algorithm of Fourier where at first variables z and (x, y) are divided. The solution is built as line

 (5)

We obtain

 (6)

Under boundary terms b_n(0) = b_n(z₀) = 0 и λ_n = nπz/z₀, n = 1, 2, 3, ..., from the first equation (6) we find

 (7)

Then, from the second equation (6) in polar coordinates (φ, ρ) we define a solution of the view

a_n = Ф_n(φ)•Ψ_n(ρ).

We obtain the system

 (8)

From the first equation (8) while γ_n = m², m = 0, 1, 2,... single periodic solution in shape of harmonic superpositions

 Ф_nm(φ) = A_nm cos(mφ) + B_nm sin(mφ). (9)

With each focused n the second equation of the system (8) always has an integral as a line

 (10)

That is absolutely and equally met in circle |ρ| < R under whole values of parameter m. To calculate coefficients of the degrees of the sedate line (10) let us build recurrent formulas

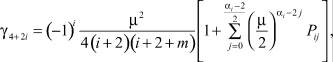 (11)

where

   , (12)

and while i ≥ 2

 (13)

The solution of the equation (3) in cylindric coordinates will look as:

 (14)

Degeneration into trigonometric line of the given function on the surface  function

 (15)

Let us define the values of Fourier coefficients:

 (16)

The convergence of the line (15) is proved with a principle of maximum for elliptic equations.

Multiple polynomials

To boost the process of calculating coefficients of P_ij(m) line (10) let us introduce auxiliary functions [5]

 (17)

That represent simplified modification of the multiple polynomials (13).

Then for whole nonnegative values l ≥ 1, i > 2 + 2l, τi sequence of multipliers into summands of function Q_i,l with similar values of l can be written as block matrixes of triangle shape. For example, while l = 1, i = 5, 6, 7 и l = 2, i = 6, 7, 8 we have summs

Q _5,1 = 2•4 + 2•5 + 3•5, Q _6,1 = 2•4 + 2•5 + 3•5 + 2•6 + 3•6 + 4•6,

Q _7,1 = 2•4 + 2•5 + 3•5 + 2•6 + 3•6 + 4•6 + 2•7 + 3•7 + 4•7 + 5•7,

Q _7,2 = 2•4•6 + 2•4•7 + 2•5•7 + 3•5•7,

Q _8,2 = 2•4•6 + 2•4•7 + 2•5•7 + 3•5•7 + 2•4•8 + 2•5•8 + 3•5•8 + 2•6•8 + 3•6•8 + 4•6•8,

to which will correspond the matrixes

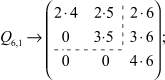
In connection with this characteristic functions Pi,l(n) are called multiple multinominals of triangle form.

Resume

While modeling physical processes in extreme conditions the most basic and difficult stage is the correct setting of an objective. In this work we have obtained the terms that provide for existence and uniqueness of the solution of the first boundary for degenerating on the line elliptic equations. During the problem research a special function class has been built and called multiple polynomials of triangle form.

1. Nesmayanov A.A., Sigalov G.F. Diffraction of small-water waves on thin body under near-critical movement speed // Young scientists' messenger. / Series: applied maths and mechanics. -SPb: Ed. SPB state technical university, 2002, №1. - Р. 72-77.

2. Sergiyenko L.S. On setting of correct objectives for degenerating models of stationary processes that take place in solenoid speed field // Non-classic equation of mathematic physics. - Novosibirsk: Ed. Institute of mathematics, 2002. - Р. 226-230.

3. Sergiyenko L.S. Mathematic modeling of physical-technical processes. - Irkutsk: Ed. Irkutsk state technical university, 2006. - P. 58-91, 169-173.

4. Sergiyenko L.S. On problem of Dirichlet for one class of degenerating on axis elliptic equations // Modern methods of function theory and adjoining problems: materials of Voronezh winter mathematic school / Voronezh state university, Moscow state university of M.V. Lomonosov, Mathematic institute of V.A. Steklovof Russian science academy: Voronezh: Ed. centre of Voronezh state university. - 2011. - P. 311-312

5. Sergiyenko L.S., Byenchayeva A.V. The first boundary problem for stationary equation of Schrodinger class // Irkuts state technical university Messenger /scientific magazine - Irkutsk: Ed. Irkutsk state technical university, 2011. - № 10. - P. 275-280.

6. Tichonov A.N., Samarskiy A.A. Equations of mathematic physics: textbook. -M.: Science, 1977. - P. 484-495, 518-527, 615-655.

7. Janushauskas A.I. Analytic theory of elliptic equations. - Novosibirsk: Science, 1978. - Р. 159-162.