A cell cycle duration is the key parameter of the cell behavior which characterise the conditions of its growth [1, 2]. Except the media, the major influence on the growth have an expression of the cell genes [3, 4] and the shifts in the intracellular molecular mechanisms [5]. Initially, it was proposed that each bacterial cell divides as soon as it reaches the so-called "initiation mass" [6]. In the later times the link between the "initiation mass" and the exact intracellular mechanism was proposed [7]: the concentration of the protein that initiates the replication of the chromosome - DnaA was strongly correlated with the initiation mass and it concentration per the oriC cite of the chromosome appeared to be constant.

According to the event of the initiation, the whole cycle can be divided on three periods [8]: C - the time from the initiation till the end of replication of chromosome, D - period from the end on replication till the division of the mother cell onto two daughters and B - period of the cycle from the birth of the daughter cell till the beginning of the next initiation. C and D periods are less variable than B [9, 10]: C+D periods were shown to have a constant duration at the fast growth (generation time is less than 1 hour) and it linearly increased with increasing the generation time above 60 min. In the slow growth, there is always B period while for the fast growth a cycle consists of the C and D periods only.

The main idea of our investigation is to bind the differences in the cell cycle structure of the fast and slow growth with the differences in accumulation of DnaA [11]. The DnaA concentration drop twice after division [12] and to initiate the replication again it have to be accumulated to the initiation level during the B period. If the concentration of DnaA is high enough, it can initiate the replication without accumulation (hence, without B period). To model the accumulation of DnaA we used the idea of the competition of the mRNAs for the ribosomes [13]: the mRNA from dnaA gene compete with the bulk mRNA. If there are some additional expressing cloned genes, this competition becomes more severe because the amount of bulk mRNA increase. This leads to more slow accumulation of DnaA and, as a consequence it lengthen the cell cycle duration. Difference between the growth rates of the cells with and without cloned genes as α = Δμ/μ result in fitness cost of the additional protein expression.

II. MODELLING THE CELL CYCLE DURATION

A. DnaA accumulation model

Assumptions of the model: 1) The level of expression of chromosome and cloned genes was assumed to be constant.The number of ribosomes was supposed to be equal for all types of cells. 2) We used the generation time т = 1 hour to separate the fast (C and D periods only, т ≤ 1h) and slow growth (B, C and D periods, т ≥ 1h). 3) The ratio of mRNA from dnaA gene to the bulk mRNA is equal to the ratio of DnaA/total protein.

We used the probabilistic approach to model the DnaA synthesis. In the course of the synthesis, all mRNAs (R_chr), some of which (R_D) encode DnaA, are distributed among ribosomes (r). Such scheme can be represented in the form of Poissons distribution [14]: ω(k) = e^-λλ^k/k!, where ω(k) is the probability that k DnaA molecules will be synthesized during one binding and λ = r R_D/R_chr. The physical meaning of this parameter is the mean amount of DnaA synthesized during one binding. Existing experiments shows [15] the DnaA/total protein (or R_D/ R_chr) linearly depends (we shall use в for the slope) on the specific rate of the bacterial population growth μ (see Fig. II A). Finally, for the cells

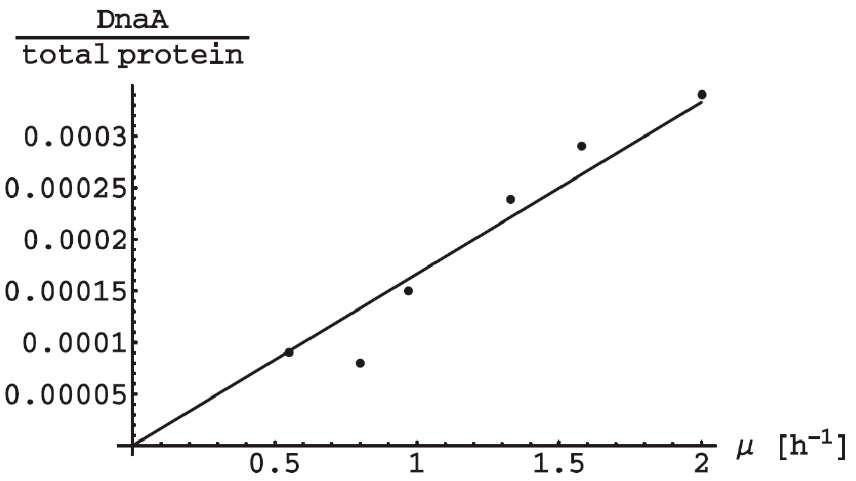
FIG. 1. The dependence of the DnaA to total protein molecule number ratio in exponentially growing E. coli cells on the specific rate of population growth. Comparison of calculations according to the model with experimental data [15]. R_D = 1, R_chr = 4288, r = 104, a = 0.72[h].

without any additional cloned genes one can write: λ^- = rR_D/R_chr *βμ. With cloned genes this equation must be rewrited with addition of cloned genes mRNA to the bulk amount: λ+ = rR_D/(Rchr + f NR_daned)βμ, where N is the number and f is the efficiency of expression of cloned genes.

The probability of synthesis of k molecules during n bindings is an n-fold convolution of Poisson distribution for one binding with itself: ω_n(k) = ωⁿ*(k) = е^-λn(λn)^к/k!. Fur­thermore, it should be taken into consideration that the bindings themselves fit Poissons distribution with respect to time with an intensity m(t). Then,

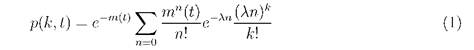
is the probability of the synthesis of k molecules of DnaA within the time t. Obviously, Eq. (1) is Neimans distribution of type A, and it can be approximated with the Gaussian distribution with the mean number of molecules of DnaA synthesized m(t)λ and variance m(t)λ(1 + λ) in the case of large m(t) [16]: p(k,t) = N(m(t)λ,m(t)λ(1 + λ)).

The parameter m(t) can be found by comparing the resultant expression for the mean number of DnaA molecules with the existing models of protein synthesis (e.g., [1]):

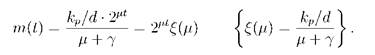
Here, k_p is the maximal rate of the elongation of the peptide chain, d = 467 is the size of the DnaA molecule (the number of amino acids) and 7 is a parameter with a dimension of rate.

Finally, the average number of newly synthesised DnaA molecules to time t as m(t)λ will be:

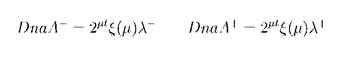
B. Calculation of the duration of the cell cycle

To initiate replication, DnaA must be activated by binding with ATP. After initiation, a DnaA+ATP complex rapidly deactivates to DnaA+ADP. To calculate the generation time we must exclude the "old" DnaA from the previous cycle - it will be the half of the amount at the end of the cycle (t = т = 1/μ): DnaA_old = 1/2ξ(μ)λ. At the fast growth with fixed duration of generation time (т = t_C + t_D = const) the initiation level Ξ for the cell without cloned genes can be calculated as

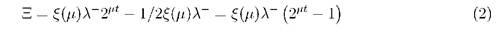
For the cells containing cloned genes, the initiation level will be reached with the delay At:

Equating (2) and (3) at the end of the cycle one can find the delay :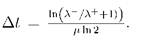

According to (т + Δt)(μ - Δμ) = 1 we obtain

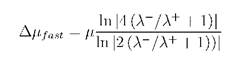
Finally for the fast growth we have the fitness cost α_fast = Δμ_fast/μ that does not depends on the growth rate if the expression of cloned genes is constant.

At slow growth the cycle separates onto two periods: constant (t_CD) and flexible (t_B) according to time. From the condition of the constancy of the concentration of DnaA accumulation of it must proceed 2^μtB times faster at t_CD period of the previous cycle than at t_B of the next. Then, to calculate the initiation level one needs to rewrite equations (2) and (3) by adding the term for B-period as follows:

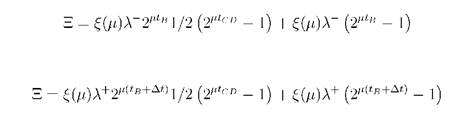
Equating these expressions together with t_CD + t_B = т = 1/μ and (μ - Δμ)(1/μ + Δt) = 1 gives the fitness cost as

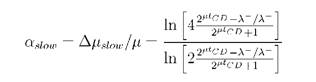
Dependence from the growth rate arise from the different structure of the cell cycle - division on stochastic and fixed periods, even if the expression of the cloned genes is constant (see Fig.IIB).

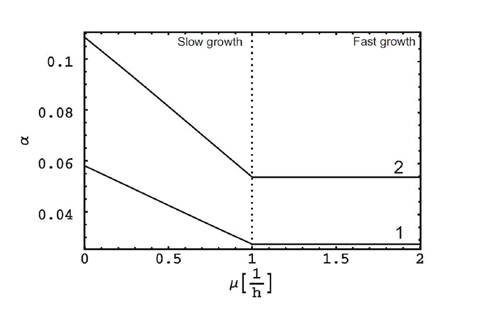
FIG. 2. The dependence of of the fitness costs coefficients from the specific growth rate of the population at fast and slow growth. Initially constant, a commence to increase with decreasing the growth rate even at the constant level of expression of cloned genes. Here λ^-/λ⁺ = 1 + fNR_cloned/R_chr, where f = 1, t_CD = 1 h, R_chr = 4288, 1. NR_cloned = 500, 1. NR_cloned = 1000.

III. DISCUSSION

The probabilistic model of accumulation of the DnaA protein makes possible to calculate the duration of the cell cycle and reveal the reasons of it alteration. In our study, the deceleration of the growth rate of bacteria bearing cloned genes is explained by the hypothesis on mRNA competition for ribosomes through the decelerating the accumulation of DnaA protein, which initiates chromosome replication. The approach proposed in this study offer an explanation of the fitness cost by exact intracellular mechanism even if expression of cloned genes does not change with slowing the specific growth rate. Our method allow to explain the different growth behavior of the bacterial cells with cloned genes and suggest a possible mechanism of the increase in the selective advantage of cloned genes free cells at low proliferation rates.

ACKNOWLEDGMENTS

Our work is supported by the grant of Federal Program "Nauchnie i nauchno-pedagogicheskie kadri innovatsionnoi Rossii" RF NK-550P2.

[2] M. Scott and T. Hwa, Current Opinion in Biotechnology 22, 559 (2011), nanobiotechnology and Systems Biology.

[3] M. Scott, C. W. Gunderson, E. M. Mateescu, Z. Zhang, and T. Hwa, Science 330, 1099 (2010), http://www.sciencemag.org/content/330/6007/1099.full.pdf.

[4] D. M. Stoebel, A. M. Dean, and D. E. Dykhuizen, Genetics 178, 1653 (March 2008), http://www.genetics.org/content/178/3/1653.full.pdf+html.

[5] P. P. Dennis, M. Ehrenberg, and H. Bremer, Microbiology and Molecular Biology Reviews 68, 639 (2004), http://mmbr.asm.org/content/68/4/639.full.pdf+html.

[6] W. Donachie, Nature 219, 1077 (1968).

[7] F. G. Hansen, T. Atlung, R. E. Braun, A. Wright, P. Hughes, and M. Kohiyama, Journal of Bacteriology 173, 5194 (1991), http://jb.asm.org/content/173/16/5194.full.pdf+html.

[8] S. Cooper and C. E. Helmstetter, Journal of Molecular Biology 31, 519 (1968).

[9] O. Michelsen, M. J. Teixeira de Mattos, P. R. Jensen, and F. G. Hansen, Microbiology 149, 1001 (2003), http://mic.sgmjournals.org/content/149/4/1001.full.pdf+html.

[10] K. Skarstad, H. B. Steen, and E. Boye, Journal of Bacteriology 154, 656 (1983), http://jb.asm.org/content/154/2/656.full.pdf+html.

[11] A. Shuvaev and A. Brilkov, Doklady Biochemistry and Biophysics 416, 233 (2007), 10.1134/S1607672907050018.

[12] L. Riber and A. Lobner-Olesen, Journal of Bacteriology 187, 5605 (August 15, 2005), http://jb.asm.org/content/187/16/5605.full.pdf+html.

[13] S.-T. Liang, Y.-C. Xu, P. Dennis, and H. Bremer, Journal of Bacteriology 182, 3037 (2000), http://jb.asm.org/content/182/11/3037.full.pdf+html.

[14] W. Feller, Introduction to Probability Theory and Its Applications (New York: John Wiley and Sons, 1971).

[15] A. E. Chiaramello and J. W. Zyskind, Journal of Bacteriology 171, 4272 (1989), http://jb.asm.org/content/171/8/4272.full.pdf+html.

[16] M. C. Teich, Appl. Opt. 20, 2457 (1981).