Introduction to a new interdisciplinary computer science research

Author revised and enhanced the theorem of structural completeness of the elementary memory of automata [1]

Every automata system, made of an elementary multifunctional digital circuits of memory (MFDC) with a complete set of transitional signals, output signals and functions of saving the system state (wherein the number of such functions are at least two) along with any functionally complete set of logical elements is a structurally complete system.

Marakhovsky’s theory of automata with multifunctional properties.

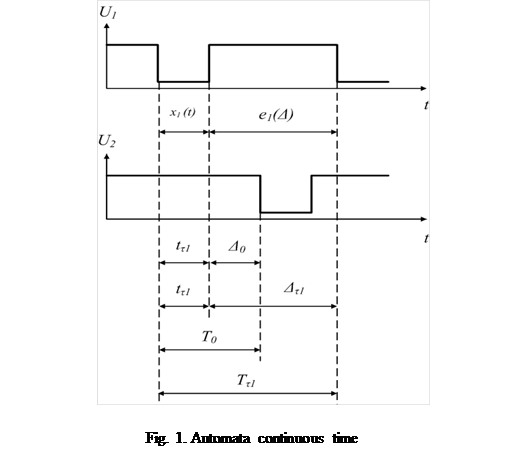
It examines the operation of MFDC in contiguous time, while the input signals x(t) and e(Δ) affect the automata’s state within a machine cycle T (Fig. 1 ) [1].

For the automata Mealy and Moore, informational input signal x(t) set the state of MFDC within a clock period t, while preserving input signal e(Δ) confirms this state within a clock period (Т = t + Δ).

The special properties of the automata M allow the input signal e(Δ) to generate an enhanced transition to a new state a(Δ) along with the function of the output signal y(Δ).

The following equations describe the functionality of the abstract Marakhovsky’s automata of different types:

1st type

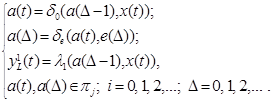(1)

2nd type

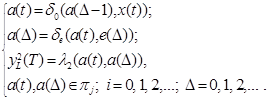(2)

3rd type

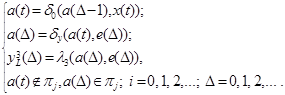(3)

The above equations completely describe the consolidated multifunctional abstract M-automata (Fig. 2).

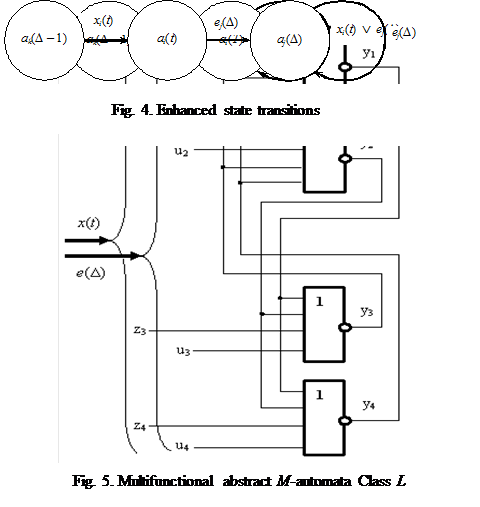
The deterministic automata 1st and 2nd types are producing unambiguous state transitions (Fig. 3), while automata 3rd type could produce enhanced state transitions (Fig. 4).

The multifunctional digital circuits of memory (MFDC)

MFDC’s internal structure allows to used at least two logical AND-NOT (OR-NOR) in each group. MFDC could change its state while is affected by two subsequent input signals x and e (Fig. 5)[1].

The theory of MFDC offers the principles and methods of building two classes of such schemes: Class L and Class Lm

The multilevel digital circuits of memory (MLDC)

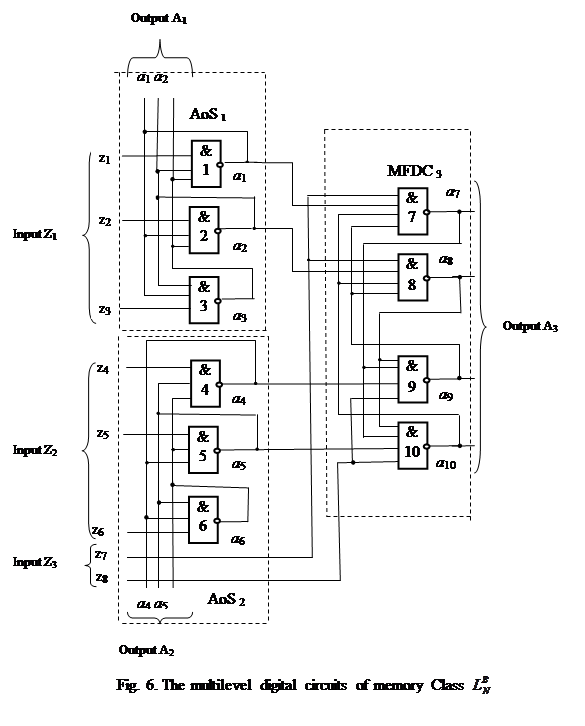
The automata of strategy (AoS) or controller is used to generate preserving input signals e(Δ) for MFDC and it could be in a form of a multistable flip-flop or the MLDC (Fig. 6) [1].

Input signals х(t) - Input Zi (i= 1, 2, 3) - are affecting the AoS and the MFDC in parallel while the AoS (within MLDC) is generating the preserving input signals е(Δ).

This would allow the AoS to process general information and the MFDC to process partial information within a single automata cycle T.

Those new features allow to tune subsets of the MFDC states within the MLDC [1].

There were proposed two types of the MLDC of classes and . For the MLDC of the class, the AoS is used not for the entire MFDC, but independently, for the each group.

The principle of hierarchical programmatic control (HPC).

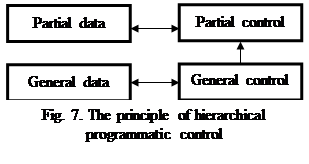
Charles Babbage proposed the principle of program management, where the information is broken down into data and data control. The author proposes the principle of HPC, where the information is divided into a hierarchy of data and control hierarchy (Fig. 7). The principle of HPC is that the general control information is used to select partial control information.

The presented principle allows changing subsets of MFDC’ states simultaneously, within a single automata cycle T.

The fourth level of control.

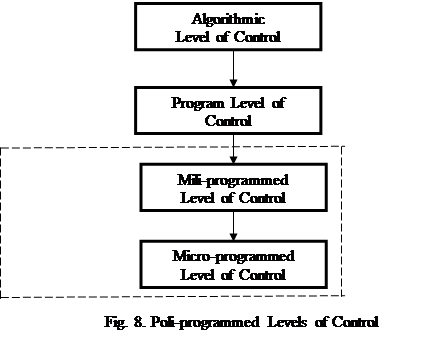
In order to build reconfigurable computing devices based on the MFDC and MLDC, the author introduces an additional, fourth mili-programmed level of control to process general information (Fig. 8).

The fourth level of control fulfills the principle of HPC and allows processing general and partial information simultaneously which is the basis to build reconfigurable computing devices based on the existing hardware components of elementary digital circuits of memory.

Standard reconfigurable devices.

The standard reconfigurable devices include: the control units, registers, counters, processors and computers [1].

Conclusion

The new technology would allow developing competitive computing systems with enhanced functionalities, another word with significantly increased machine intelligence.