The classical theory of the heat capacity of monatomic gases gives values: Cv = 1,5R and Cp = 2,5R. The quantum theory of atomic gases does not add anything. However, the reference value of Cp for argon when P = 100 bar and T = 170 ° K is 11, 8 R [ 1]. And, from 155 ° K to 170 ° K heat capacity of argon increases and then decreases with the increasing of temperature, and only at T = 1200 ° K takes on a value 2,52 R, closer to the classical one. That sort of behaviour of the heat capacity of a monatomic gas can be explained only by the cluster model of gas. Description of the cluster theory of heat capacity of gases is the aim of this work.

This model assumes that, when low temperatures and high pressures meet, gas molecules are combined into groups called clusters or complexes. This clustering process changes the number of structural units. Furthermore, each cluster has an internal energy. These factors lead to an increase of the gas thermal capacity. Although small clusters interact with each other, the impact of these interaction on the virial coefficients are compensated with the number of structural units. For this reason, the equation of the state of gases can be written in the form of Hirschfeld and Rouzvir [ 2], taking into account only the change in the number of structural units:

, (1)

where Х – is the average cluster size. Identification of the remaining quantities is conventional as in [ 2 ].

Determination of the average cluster size is a major difficulty for the use of the cluster model of gas. Having determined the probability of decay of the cluster and the capture of by it a monomer, we managed to get a system of equations establish linkage between concentrations of clusters:

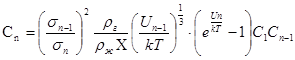, (2)

where ρg – is gas density, ρl – liquid density, σn – diameter of a dimensionality of a cluster n, Un – energy of connection of a cluster with monomer (potential barrier), Cn – concentration of clusters in dimensionality n.

If in the formulae (2) to take Un=ε, ; 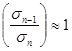, we will get , where

; (3)

, ε – parameter of the potential by Lennard-Jones. In this case, the concentrations of the complexes make a decreasing geometric progression, the sum of which can be easily calculated. In condition, that , it is coming out

. (4)

The average size of a cluster can be calculated very easy:

; (5)

that is . Where Х is a part of q, then equality (5) leads to a quadratic equation which relates to X and after solving, we can get:

, (6)

where .

Equality (5) makes it possible to find a connection between derivatives and :

. (7)

Derivative was calculated in [3].

Furthermore, using equality (1) we can determine the free energy, then internal energy, and enthalpy of a gas:

; (8)

; .

In accordance with formulae; we can get:

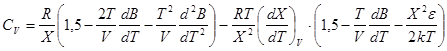; (9)

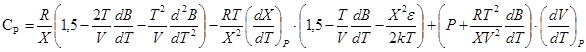, (10)

where

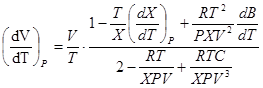. (11)

Calculations made by formula (6), (7), (10) and (11) yield the following results: when Т=170°К and Р=100 bar СР=12,135R, the margin of error in comparison with [1] less then 3%; when Т=300°К – the margin of error is about 3%. It should be mentioned, that neither the model of Van-der-Waals, nor model of Lennard-Jones with virial equation of a state give results like these. Even when Т=300°К , the model of Van Der Waals has an error of 19% and when low temperatures, has more then 50%. Model of Lennard-Jones, when Т=170°К has an error with determination of СР more than 250%, and when 180°К – 10%. This shows that despite the complexity of the use of the cluster theory, it agrees well with the known data by СР.

2. Hirschfelder, J., Kartiss H., Bird R., Molecular theory of gases and liquids. - Moscow. Lit.,1961-930S.

3. Pavlov A.M. Complexes of molecules and their effect on the properties of gases. - Ust-Kamenogorsk, Vol. EKSU. S. Amanzholov, 2012 - 282c.