To develop the mathematical model for evaluating the distribution of components in the molten cast iron during centrifugation, let’s consider the well-known equations describing the process of mass transfer in a centrifuge cell taking into account the diffusion and sedimentation for 2-component mixture [1].

We assume, following [1], that the mixture consists of two components. In the process of centrifugation particles move under the influence of inertial force. The change of drm/dτ radial coordinate at the midpoint is conventionally accepted as the U border movement speed.

The process of mass transportation in the centrifuge is described by the Lamm equation [2], which is given for the radial sector cell as

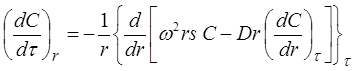(1)

where ,are the derivatives of concentration (kg to l) at constant values ​​r and , respectively, D is a diffusion coefficient [m2 s], s is a sedimentation constant which characterizes the rate of sedimentation of particles per ω2r centrifugal acceleration unit.

This equation, as shown in [2], has not, in general, the exact analytical solution. However, for two ultimate cases there are exact solutions: for D = 0 (no diffusion), and s = 0 (no sedimentation). Since we are interested in the case when the effect of diffusion compared to the inertial forces is little, we consider the solution of equation (1) with D = 0.

Taking into account the Fick equation, which describes the process of diffusion and sedimentation of the section border in an infinite stream in the direction perpendicular to the axis of rotation OX [2],

with D = 0 we get ,

where is a section border (meniscus), and taking into account (1), we find

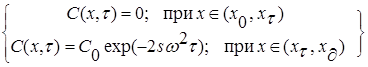(2)

where is a starting coordinate of the mixture section border (meniscus), m;

is a coordinate of the melting pot bottom, m; is initial concentration, kg to l.

The concentration distribution by time in this case has the plateau area with a constant concentration. The essential feature of such a solution is that particles of a corresponding component with a higher density are eventually concentrated on the lateral surface of the melting pot and the lower density components are distributed along the lateral surface of the preceding component.

Taking into account the ultimate solution of the Lamm equation (2) and the fact that the assigned task of the distribution of the component by volume when does not require knowledge of the process background, we can reduce it to a fairly simple algorithm. Let the form of the melting pot is given by the equation

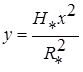, (3)

where , are the constants which are the coordinates of arbitrary point on the boundary of the section.

We are putting in order the components of the mixture by increase of given (when ) densities and give the corresponding mass concentrations of the mixture components at the initial time .

During centrifugation molecules of the component move under the influence of artificial gravitational field and after a certain time, according to the particular solution of the Lamm (2), will be located in layers. We assume that the speed of rotation of the melting pot is limited by both the top and bottom so that the contents of the melting pot is not formed a gap in the vicinity of the axis and inertial forces exceed gravitational ones.

To determine the boundaries of mixture components the method of successive approximations has been developed.

For the particular case of Fe-C-S three-component mixture with the concentrations equal to C, Fe - 92.45%; C - 5.1%; Si - 2.45%, the total mass M0 = 100 g and the given shape of the melting pot H*=12см, R*=3,6см the calculations has been made, results of which, after triple iterations, are shown in Table 1.

Table 1

Table of calculations results

Here, rk, Hk are the coordinates of the upper boundary point of the «k" indexed mixture ().

2. Lamm, O. (1929) Akr. Mat. Astr. Fys., №21, С.1–2.