Introduction.

The important directions of development of continuous casting of metals are improvement of billet quality and near-net-shape casting. The horizontal continuous caster with electromagnetic levitation, realizing these directions, is described in work [1]. On this caster the liquid metal stream, leaving a nozzle, keeps horizontally by a field of electromagnetic forces. This field is created at crossing of the constant magnetic field and the direct electric current. The scheme of caster is given in Fig. 1.

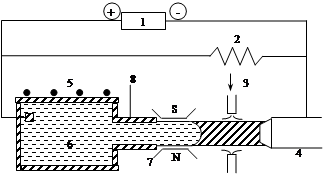
Figure 1– Schematic view of horizontal continuous caster with electromagnetic levitation (top view): 1 – DC current supply; 2 – resistance; 3 – cooling gas; 4 – electrode; 5 – heater; 6 – molten metal; 7 – pole; 8 – nozzle.

This caster allows to make small billets with a pure surface because the melt has no contact with mold wall. It is considerable advantage in comparison with other machines for near-net-shape casting.

In work [2] the condition of levitation of a liquid metal stream is given by:

,

where – magnetic induction, i – current density in stream section, – density of liquid metal, – acceleration of gravity.

This condition is rightly only for uniform magnetic fields. In actual practice the magnetic induction field is non-uniform on stream section.

Material and methods.

Figure 2 shows the location of a metal stream section which axis coincides with the center of an electromagnet working gap.

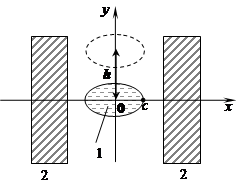
Figure 2– Schematic illustration of the metal stream location in the electromagnet working gap:

1 – metal, 2 – pole; h – height of metal stream location, 2с – stream width.

The maximum values of induction are observed in the center of the gap. Then, to edges of poles along an axis у, induction value decrease. In this regard the location of the stream section in the gap center unstably. Therefore the axis of the stream section has to be above the gap center on the set distance h.

In this regard we write the levitation condition as:

, (1)

where – horizontal component of a vector of the induction in stream section, S – area of the stream section.

The integral in the left part of expression (1) we can rewrite as:

,

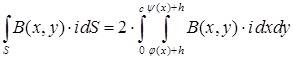where – mathematical description of the lower and upper bound of the stream section (Fig. 2).

Further defined function:

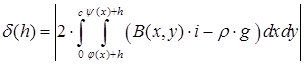. (2)

Such value at which function is minimum will be required value. It is supposed that distribution in the electromagnet working gap is received by experiment or by calculation.

Results.

This calculation procedure was tested by comparison of experimental and calculated values of . Experimental measurements were carried out on physical model of the electromagnet of caster. As an electromagnet used constant magnets. During experiments was carried out levitation of an aluminum plate 12,7 cm long and with a section of 5´1 mm2. Direct current on the plate gave from a DC current supply B5-47/1. During experiment varied the current I from 1 to 3A with a step 0,5A at electric potential U=9,9 B. Figure 3 gives the results of modeling of height of the plate location.

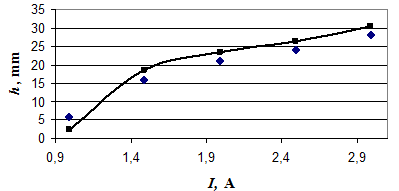
Figure 3–Comparison of calculation and experimental data on levitation of the aluminum plate in magnetic field: - the values of height received by means of a Eq. (2),

- the values of height measured experimentally.

As we can see in Fig. 3, calculation and experimental data coincide. The difference on the average does not exceed 10%. This difference in experimental and calculation data can be explained with heterogeneity of the magnetic field on length of the electromagnet poles of experimental installation. As a whole, comparison of experimental and calculation data showed that the formula (2) can be used for forecasting of location of the metal stream in the working gap depending on the current, given on billet, and the magnetic potential of the electromagnet.

By means of this method of forecasting of location of the metal stream in the working gap research is executed on the example of receiving aluminum billet of rectangular section 5×10 mm2. During research varied values of current density and magnetic potential of the electromagnet which defines the size of the magnetic induction in the working gap. Distribution of magnetic induction in the working gap calculated by means of mathematical model [3]. Figure 4 gives the results of research.

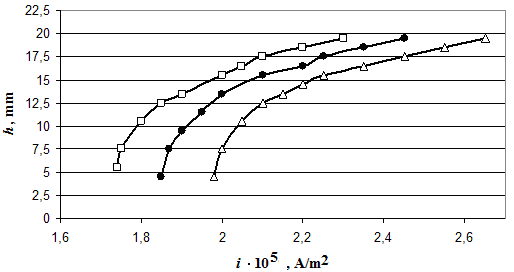
Figure 4–Dependence of height of the metal stream location in a working gap from current density at various magnetic potential of electromagnet:

– 1400 At, – 1500 At, – 1600 At.

With increase in current density in the stream there is an increase in height of location of stream in the working gap. In the range of 5-14 mm even little change of size of current density leads to considerable change of height . Then at increase in current density on 0,2·105 A/m2 height increases evenly on the average by 2,5 mm. This is due to the fact that at mm induction in the working gap decreases therefore the increase in current density influences height less effectively.

Conclusions.

The received results can be used for substantiation of technological parameters of horizontal continuous caster with electromagnetic levitation. Graphic dependences allow to determine the necessary current density in the stream and magnetic potential of electromagnet providing the location of stream at the preset height.

2. S. Takeuchi, J. Etay, M. Garnier Stability analysis of free surface of liquid metals levitated by electromagnetic force// ISIJ International, vol. 29 (1989), # 12, p. 1006-1015.

3. Kabakov Z.K., Mazina I.Y. The mathematical description of magnetic field in the working gap of electromagnet// collection of articles of the All-Russian scientific seminar "Scientific and technical progress in metallurgy"(November 28-29, 2011) – Cherepovets: Cherepovets state university, 2012.– p. 91-97.