Introduction.

For the calculation of the thermal state of the roller continuous casting machine we need to know the specific heat flux transmitted by radiation from the slab surface area per unit surface of the roller and, in particular, the local angular coefficient. Typically, for definition of this ratio uses a formula derived in the work of G. Bauman [1]. In deriving this formula does not take into account the fact that some of the radiation flux from the surface of the steel slab is screening by adjacent roller.

Material and methods.

In this paper, the formula for calculating the local angular coefficient is derived taking into account the screening effect produced by the adjacent roller. In addition, the term of elementary angular coefficient for the two-dimensional radiative heat case transfer [2] was used during formula derivation. Thus we avoid double integration.

Figure 1 shows a scheme to the conclusion formula.

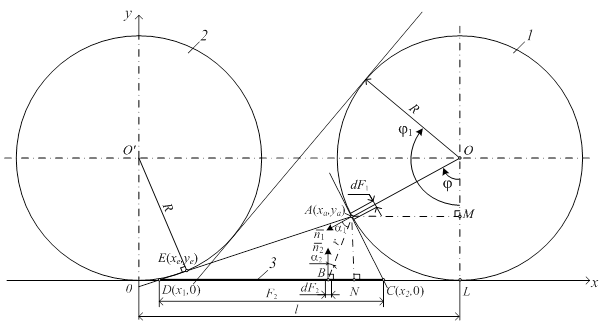
1 – main roll, 2 – adjacent roll, 3 – slab surface ()

Figure 1 - Design scheme for determining the angular coefficient of the radiation from a slab to roller elementary area

The roller with center O contains elementary area , which emit elementary areas , located on a segment of the slab DC. Vectors and are normals to the и , respectively.

We define the local angular coefficient (slope) of the , using the well-known formula:

(1)

Taking into account the substantial slab width and a small distance between the rollers used to determine the elemental slope formula, derived in [2] for the case of two-dimensional radiative heat transfer:

(2)

We define the point’s coordinates: А(xa, ya), С(x2, 0), D(x1, 0) и Е(xe, ye) (fig. 1):

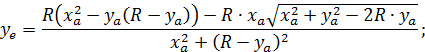
Given the scheme (fig. 1), we obtain the expression:

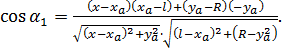(3)

We find from the triangle :

(4)

Substituting (3) and (4) into (2):

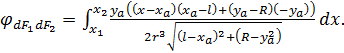(5)

After integration we obtain the required local slope of the radiation from the slab per unit surface of the roller (the full derivation is not presented for reasons of reducing the amount of this article):

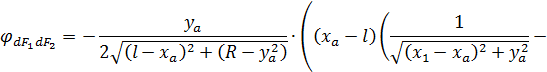
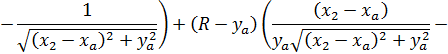
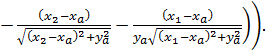(6)

The value of the degree of radiation shielding from the adjacent slab roller depends on . When formula (6) is converted to a well-known formula G. Bauman’s [1]:

(7)

Results.

The calculation results by formulas (6) and (7) are shown in Fig. 2 with l/d=2 (a) and l/d=1 (b) (l – distance between the rollers axes, d=2R – diameter of roller’s drum). The calculation used the raw data corresponding to the experimental conditions [3]: d=0.22 м; l =0.44 м; и d=0.44 м; l =0.44 м.

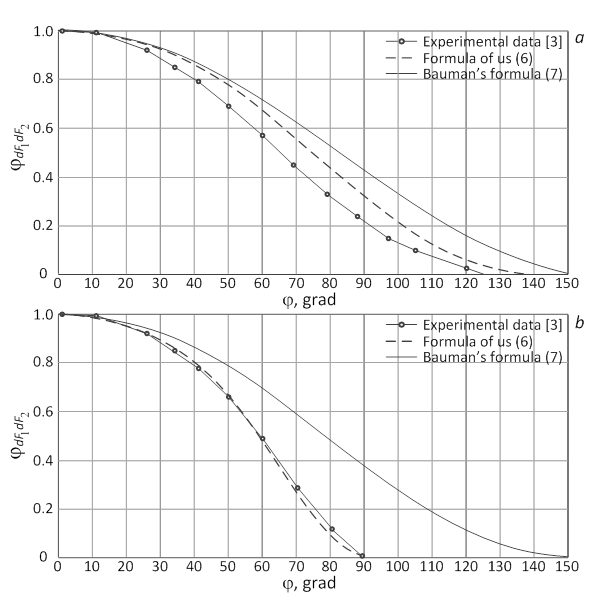
Figure 2 – Dependence of the local angular coefficient of thermal radiation from the slab surface per roller unit surface on angle with l/d = 2 (a) и l/d = 1 (b)

Fig. 2 (a) shows that at low shielding degree (l/d = 2), the maximum difference between the results of experiment and calculation by the formula (6) is about 10%, and the formula (7) – 20%.

As we can see in Fig. 2 (b) with l/d = 1, the calculation results according to formula (6) and experimental data are almost the same. The difference between the calculation results using G. Bauman's formula, which is about 40%, due by maximum degree of radiation shielding by adjacent roller at l/d = 1, i.e. with no gap between the rollers.

For the curved slab caster l/d ≈ 1.1, so the calculation of heat transfer between the ingot surface and the roller we are recommends to use the formula (6), where takes into account the screening effect radiation from the slab by neighboring roller.

Conclusions.

Thus, based on the theory of two-dimensional radiative heat transfer, we solve the problem of the radiation local angular coefficient from the slab surface between the rollers on arbitrary elementary area of ​​the roller surface with the screening of the adjacent roller. This solution differs from the known radiation screening effect by adjacent roller and recommended to refine models of the thermal state of caster rollers.

2. Z. Kabakov, N. Sinitsyn. The calculation of the slopes of the radiative heat transfer between the walls of an infinitely long channel // The successes of modern science. Scientific journal of the theoretical and experimental problems in the natural sciences. – 2002. # 5. – p. 85.

3. N. Thelin. Heat and mass transfer in the "roller-processed metal". Thesis for the degree of Doctor of Science, Cherepovets, 2005.