The reduction of nonlinear geophysical tasks to the equation of sine-Gordon

, or , (1)

is connected with its complete integrability [1-3] allowing to find solutions that describe interaction of solitary waves called solitons in explicit form.

The equation of motion (1) with the periodic load consideration can be written in the following form:

, (2)

where is the variation of the periodic potential, . For example, is for the model of elastic blocks interaction, where is the coefficient of friction in the periodic force absence [5]. If the interblock environment is heterogeneous, the equation of motion (2) can be presented in the following form:

, (3)

where, is, for example, the friction force potential , ... b=L/2n, where L is the linear block size, n=1, 2, 3,…., b is the linear inter-bloc size of heterogeneity.

Let us consider geomechanical model (Fig. 1) for the to demonstrate the interaction of the block when exposed to an external load F(m,v). The physical properties of faults (f) and blocks (m) are not visible in case of its consolidated state. The pulse influence of the force F(m,v) on one of the blocks will lead to a separation of the boundary block (blocks) at any length of the blocks chain, id est with the parameters of L=d·n, (d is diameter of the block, n is the block quantity), each external action F(m,v) can be compared to any earthquake. During the period of disintegration the local deformation of bloc environment separate parts is possible and, thus, one and the same system of units may react differently to the same external exposures at different periods of observation. The ratio of the periods of consolidated and unconsolidated state is defined by the processes in the earth's crust. In its motion the block will only interact with two side blocks that determines the type of the motion.

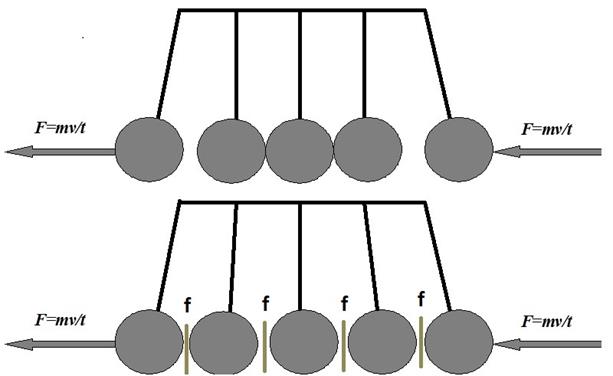
Fig. 1. Geomechanical model of the interaction of crustal blocks

Map legend: m is the Earth crust block; F(m,v) is the pulce (periodic) load; f is an interblock suture zone.

In its general view the solution (1) in the form of a kink or topological soliton has the following form: , where = ±1 is topological charge of kink. = +1 is called kink, and = -1 is called antikink. The parametric variable v is the speed of the kink, where причем its value must not exceed the speed limit equal to 1. One more solution of the sine-Gordon equation is called breather or dynamic soliton.

Due to the nonlinear properties of rock massif there is an additional deformation блока, . The voltage in the nonhomogeneous bodies depends on the speed of deformation and for them the equation can be presented in the following form [7]

where is the speed of transverse elastic waves, ρ is the density of a solid body, is the constant determining the stress relief. =2·10-6 см/с (60 см/год) is the same for all the rocks. With the constant speed of deformation the solution of the equation (10) can be presented in the following form [7] . With the course of time the stress of nonhomogeneous body changes in the limits of . Generally the calculations of excess stress on the body for arbitrary speed of deformation (including with account of nonlinearity) can be calculated by the formula 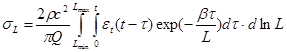, where Q is a mechanical quality of the material, determined through the attenuation of the oscillations, which is of the order of 102in the Earth lithosphere; Lmin and Lmax are the sizes of the minimum and maximum of inhomogeneities contained in the considered volume of the environment.

Thus, in cases of rotational and vibrational one-dimensional motions of a homogeneous block chain the problem is reduced to the analysis of solutions of the sine-Gordon generalized equation (3) in the presence of small external perturbation investigated in the work [троф].

[2] V.G. Bikov, “Nonlinear wave processes in geological environment”, Dal’nauka, Vladivostok, 2000.

[3] R. Dodd, G. Alebeck, G. Gibbon, H. Morris, “Solitons and nonlinear wave equations”, World, Moscow, 1988.

[4] S.V. Trofimenko, “Tectonic interpretation of the azimuths anomalies statistical distributions of Aldansky shield potential field”, Tikhookeanskaya geology, Vol. 29, №3, 2010, pp. 64-77.

[5] S.V. Trofimenko, N.N. Grib, “Geomechanical model of the Earth’s crust block movement”, Contemporary issues of science and education, №3, 2012. http://www.science-education.ru/103-6462.

[6] S.V. Trofimenko, N.N. Grib, Simulation of Interaction Crustal Blocks Using Pendulum Newton // World Applied Sciences Journal 22 (11): 1550-1553, 2013. DOI: 10.5829/idosi.wasj.2013.22.11.13016

[7] V.V. Adushkin, “Actual problems of the Earth crust geomechanics", Herald of the DGGGMS RAS, № 1(16) , 2001.