Designing and building of a surface of the tunnel demands considerable time and expenses. Therefore perfection of methods of designing of surfaces of underground constructions is an actual problem in mine structure. All know, that tunnel surfaces is a difficult curvilinear surface which should correspond to beforehand set requirements.

In стати the new method designing of a surface of the tunnel on beforehand set conditions with use of biquadrate transformation of plane L which allows to describe designing of each section of the tunnel by one equation is stated.

1. A way of reception of curves with use of biquadrate transformations L

The surface section can be set in the various ways [1]. In an offered way of a prototype (curve) is exposed to geometrical transformation L, therefore the image (a required curve п/) [2] turns out. Thus the prototype is set by the equation:

Where: k, m – constant factors.

Biquadratic transformation L8 is set by the equations:

, ,

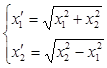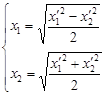where: х1/, h2/-co-ordinates of points of an image;

х1, х2 - co-ordinates of points of a prototype.

The equation of the received curve p/registers in a kind:

,

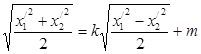Where: k, m – constant factors.

2. Designing of a surface of the tunnel on the set parametres

The essence of transformation consists in the following. We take some points of a prototype п in conformity, then each of these points us subject to transformation L (fig.-1). We will find sets of points, smoothly having connected which have received a curve an image of the item / thus the curve form n/depends on values of factors m, k an item prototype

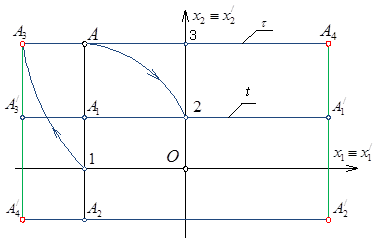
Fig. - 1

The tunnel surface is formed as a result of moving of a flat curve of the fourth order (section) on an axis of a directing curve.

Using graphic model of biquadratic transformation L we design the form каналовой tunnel surfaces as follows:

1. Initial data for the decision of this problem are an axial line channel surfaces of the tunnel and laws of change of parametres of cross-section sections a and b (fig-2 and fig-3).

Each cross-section section n/ the tunnel is the curve of the fourth order received with use of biquadratic transformation L. Thus parametres a and b each cross-section section are defined from formulas:

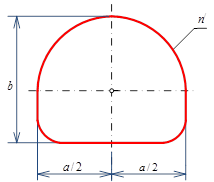
Fig. – 2

, (1)

Where: l – distance from the beginning of the tunnel to considered cross-section section.

2. We use the biquadratic transformation L set by the equations:

(2)

Where - co-ordinates of a point of a prototype;

- co-ordinates of a point of an image.

3. As a prototype we accept general provisions straight line п which equation looks like:

(3)

Where k, m – constant factors.

Fig -3

4. We define factors k, m the equations (3). For this purpose we use properties of biquadratic transformation L:

Point – a prototype B and a point – an image В2/have identical height. Point В2/is essay a point of section of the item / therefore a point B a prototype п has co-ordinates (fig-4):

(4)

(5)

The point – a prototype C will be transformed to points – images С1 / = С3/and С2 / = С4 / which lay on axis Ох1. Point С1/has co-ordinates (b+c; 0). To point С1/there corresponds a point with which co-ordinates satisfy to a condition:

(6)

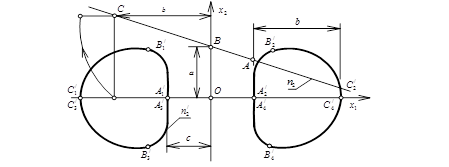
Fig – 4

Let's define co-ordinates of a point of C. From a course of construction of point С1/, it is possible to receive a following equation:

, (7)

Where: with =.

Considering a condition (6), from the equation (7) we will receive

Or

(8)

The prototype п passes through points В and С. Тaking into account it is worked out the following system the equation:

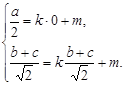(9)

Having solved this system of the equations, we will receive:

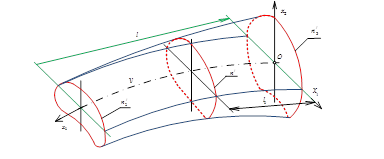
(10)

. (11)

5. Subjecting a prototype п to biquadratic transformation L, we receive required section of the tunnel which satisfies to beforehand set conditions. The algebraic equation of this section looks like:

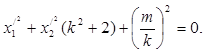(12)

Where: k, m – the parametres of a prototype described by the equations 10 and 11.

The parametrical equation of section of the tunnel looks like:

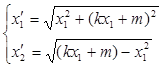, (13)

Where: х1 – parameters ;

..

6. Similarly, we design any demanded section of a considered surface of the tunnel (fig-5).

Fig – 5

7. The equation channel tunnel surfaces registers in a kind:

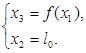(14)

Where f (х1) – the function describing a contour of cross-section section of the tunnel;

lo – distance from cross-section section prior to the beginning of the tunnel, х3begin≤lo≤x3end.

Thus, the offered method of designing with use of biquadratic transformation allows to receive various classes channel surfaces and to define the equation of family of cross-section sections of a considered surface that facilitates the further geometrical calculations on the COMPUTER.

2. Nurmahanov B.N., Bajdabekov A.K., Mahanov M. M, Usupov M. M, Карымсаков U.T.development of the theory of geometrical transformations and their application. – Taraz, TarGU. 1999. - 136 p.