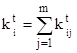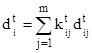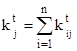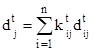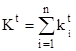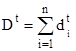Introduction. Wildfires destroy biodiversity, increase desertification, affect air quality. They have negative effect on human life and health, human property and wellbeing, cultural and natural heritage, employment, recreation, economic and social infrastructures and activities. It has widely recognized that prevention is the most effective approach to face wildfires. Rescue plans should be established in advance to consolidate various forest protection measures, maintain fire-prevention and fire-fighting facilities and equipment, properly train fire-fighting units and increase mobilization ability.

The data domain characters. Decision-making in wildfire prevention is based on the huge amount of knowledge which describes complicate interdependencies between physicochemical, biological, social and economic processes. Moreover, these processes are characterized with stochastic behavior, spatial and time dependency. Wildfire prevention is a critical domain where incorrect management decisions may have disastrous social, economic and ecological consequences [1, 2].

Complexity of decision-making in wildfire prevention [1].

1. Spatial dependency.
2. Uncertainty or approximate knowledge [3].
3. Variability of the processes nature. A decision-maker has to make decisions in a changing environment with limited time resources.
4. The presence of both quantitative and qualitative parameters which characterize wildfire dynamic.
5. Application of special methods, such as expert assessments, fuzzy sets, etc. for assessment of quantitative parameters. These methods are characterized with certain level of subjectivism [3].
6. The complexity of formalization.

The features of the data domain listed above reflect the complexity of decision-making in wildfires prevention and require the development and implementation of new models, methods and information technologies capable to process not only numerical parameters but also the experience of experts.

The features of the data domain allow to assign the tasks connected with decision-making in wildfire prevention to weakly formalized. Strict analytical methods don’t correspond the level of severity of their formulation. So there is a need to apply the intellectual methods to the tasks of decision-making in wildfire prevention.

The goal of the article. A decision-maker has to analyze huge amount of information when making decisions under conditions of uncertainty. In such cases decision-makers often make a decision based on previous experience and knowledge of general laws of wildfire dynamic. The existent level of development of intelligent decision support systems allows to decide decision support tasks in complex weekly structures dynamic systems.

The purpose of the paper is to describe a new hybrid approach to creation of the fire prevention system. This approach is a combination of model-based reasoning and scenario-based reasoning.

The choice of the artificial intelligence (AI) methods. The field of AI can be divided into two parts such as strong AI and weak AI. Weak AI is not intended to match or exceed the capabilities of human being. Strong AI matches human intelligence. It’s aimed at performing any intellectual task that human being can. Strong AI systems use real reasoning and rationality when making decisions. Weak AI methods can be applied to a wide range of problems but they are not necessarily incorporate any real knowledge about the world of the problem that is being solved. Weak methods are designed for the whole classes of subject areas. In contrast, strong methods are focused on the information specific to each subject area. They depend on a system being given a great deal of knowledge about its world and the problems that it might encounter [4, 5]. It’s clear that knowledge representation in the area of wildfire prevention requires strong AI methods.

Despite the fact that the data domain is weakly structured we can identify subtasks which can be solved analytically with some degree of accuracy. These are such tasks as fire danger assessment, the modeling of wildfire dynamic, fire risk assessment. At present there are a lot of works aimed at the solving of such tasks [5, 6]. The article presents the deterministic-probabilistic model of fire danger developed by Baranovskiy N. [7] and the model of fire risk assessment [8] improved by Zharikova M. We used the existing model of fire dynamic to model wildfire behavior. The system also uses the model of wildfire damage assessment. Fire damage for each homogenous forest area is determined as the cost of burnt wood. In order to fit the analytical models of separate subtasks in the overall system we are going to use model-based reasoning (MBR) [9]. To be able to forecast a wildfire behavior under a variety of natural and meteorological condition we are going to use scenario modeling [10].

So, this article is focused on the combination of the methods of MBR and scenario modeling for creation of wildfire prevention system.

The analytical models used in the system. The system uses such models as a deterministic probabilistic model of fire danger assessment, a probabilistic model of fire risk assessment, a wildfire dynamic model and a model of wildfire damage assessment. Consider the first two models.

Deterministic probabilistic model of fire danger assessment. Suppose that a range of events of wildfire occurrence for various reasons are as follows: A1 – arson, A2 – careless handling of fire, A3 – agricultural burns, A4 – the impact of the railway, A5 – the impact of power lines, A6 – oil spill burning, A7 – the impact of highways, A8 – falling of the stage of the rocket, A9 – accident at the technological facilities located in the wooded areas, A10 – fire caused by a solar radiation focused by a glass bottle, A11 – a cause is not established, A12 – fire caused by lightning. According to the probability theory [11] the total probability of fire occurrence as a result of combination of factors can be determined by [7]:

, (1)

where P(FFi) is a probability of wildfire occurrence for specific reason.

A probability of human-caused fire occurrence is determined as follows:

, (2)

where P(A) is a probability of anthropogenic load,

P(Aj,i/А) is a probability of fire source from anthropogenic cause providing that the forest area was visited on week day j, P(FF/А,Aj,i) is a probability of forest fire on day j from anthropogenic cause. This probability is determined by the formula , where P(D) is a probability that forest fuel (FF) is dry enough, P(Ii/D) is a probability of ignition of FF by sours i providing that FF is dry enough.

А probability of forest fire from thunderstorm activity is determined by the formula [7]:

, (3)

where P(L) is a probability of dry thunderstorms, P(Lk/L) is a probability of ground lightning discharge for the kth hour of a day on the assumption of passing thunderstorm, P(FF/L,Lk) is a probability of forest fire for the kth hour of a day on the assumption of passing thunderstorm, which is determined by the formula , where P(D) is a probability that FF is dry enough, P(IL/D) is a probability of FF ignition by ground lightning discharge providing that FF is dry enough.

A probability of forest fire beginnings from solar radiation focused by a bottle is determined by a formula [7]:

, (4)

where , P(I11/D) is a probability of FF ignition by focused solar radiation source (it’s determined empirically or numerically). P(D) is determined using deterministic model of FF layer drying under the influence of external conditions [12].

Probabilistic model of fire risk assessment. When modeling of fire risk we will consider the objects affected by the fire and the fire itself.

Oblects are all static natural or man-made entities considered as endangered by wildfire. Let us denote with , i = 1, …, I the set of objects, where I is the number of the objects in the forestry.

Let us call the initial data the natural (characteristics of the forest, topography) and meteorological conditions.

Restrict the number of possible fires at the forestry. Let , i = 1, …, I denote the set of possible fires, where Si is a fire the source of which is on the object oi. At that is the condition of fire the source of which is on the object oi, at the time moment t. , i = 1, …, I.

Forest fire risk for a certain object at a certain time moment is a multiplication of the probability that the object will burn and the value of estimated damage from fire.

A set of objects Oj = {o1, …, on} suffered from fire Sj, consists from the objects of different nature such as buildings, roads, forest plants. Each object must have an impact function that defines the magnitude of modifications with respect to the hazard’s impact [13]. We are interested in damage to the object. So the function will show damage. Let us call this function damage function. For each pair (object оiOj, fire Sj) at a certain time moment we determine conditional individual impact probability (the probability that object oi is affected when the fire Sj is known to have happened) and individual damage . is determined with the help of the fire dynamic model аnd is determined with the help of the damage assessment model. If a probability pj of forest fire Sj occurrence is known, we can determine individual impact probability , which is the probability that the object will be affected by the fire Sj at the time moment t [8]:

= * pj. (5)

От the basis of this basic relation we can determine risk for both the given fire and the object. The first is called the collective or scenario risk, the second is the individual risk.

Individual risk deals with one given object affected by a risk. This object can be affected by a set of fires. The impact probability expresses a probability that the object oi is affected by any fire from the set S considering m independent but mutually not exclusive fires Sj. This probability is given by [7,8]:

. (6)

The expected damage at the time moment t for the object oi is determined as the weighted sum of all individual expected damages :

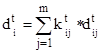. (7)

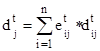Collective risk deals with a given fire which can affect a set of objects. A probability of a fire occurence pj is a probability that a given fire will occur. The expected damage at the time moment t for each jth fire is a weighted sum of the expected damages of all objects [8]:

. (8)

Collective influence probability is determined by a formula:

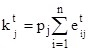. (9)

Collective fire risk is determined by a formula:

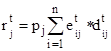. (10)

The weighting is done with the impact probability. This is a probability that a fire will reach and affect an object. Objects lying inside the perimeter have an individual impact probability of 1.

A sequence of fire risk calculation is as follows. First, a probability of ignition for each forest area is determined based on a model of fire occurrence, taking into account given initial data. Then, a certain fire is considered. The influence probability is determined for each object affected by the fire using the forest fire behavior model. We used the model of Rothermel adapted for the forests of the former Soviet Union [14, 15]. Next, a sum of damage caused to each object by the given fire is estimated. Finally, the resulting parameters are combined in a risk matrix that displays the relationship between all possible fires and objects for a natural and meteorological conditions [8]. The described model allows to determine the spatial distribution of the probability of fire and fire damage. The output data of this model are contained in a risk matrix which is built for each combination of initial data and at given time moment t (table 1).

Table 1

Risk matrix for given initial data at the time moment t

Where:

Sj – fire,

oi – object,

pj – conditional probability that fire Sj takes place under given initial data,

– probability that object oi is affected by fire Sj at given time moment t,

– damage caused at object oi under the condition that the fire Sj reaches the object at given time moment t,

– probability that object oi is affected by any fire at given time moment t,

– expected damage caused by all fires at object oi at given time moment t,

– expected number of objects that will be affected by fire Sj at given time moment t,

– expected damage caused by fire Sj at all objects at given time moment t,

kt – expected total number of objects affected by forest fires under given initial data at given time moment t,

dt – expected total damage caused by fires at given time moment t.

Initial data are the global conditions that influence the risk for the whole examined forest area. The influence probability and expected damage are determined for each pair fire-object at the given time moment t. With the help of risk matrix for each object oi wу can obtain the probability that the object at any time moment t will be affected by any fire () as well as expected damage (). For each fire Sj we can calculate expected set of objects that will be affected by the fire () and the total expected damage ().

Scenario modeling. Let us call scenario a purposeful model describing a dynamic of a situation as a sequence of states at definite time moments [16]. A scenario allows to represent the consequences of different trajectories of system movement. The article deals with a model of scenario-based reasoning as applied to forest fire protection system.

Suppose X is a finite set of the system state parameters, Val(X) is a set of parameter values, , where Val(xi) is a value area of parameter xi.

Let us call a system state С a set of parameter (factors) values, 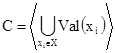[16].

Let us denote a set of possible system states by W. Then a certain system state can be described as follows [16]

, (11)

where – a set of environment parameters that don’t depend on object parameters;

– a set of objects;

– a set of object parameters;

– a set of relations between objects.

– a set of alternatives.

The graphical interpretation of the notion of the fire scenario is depicted in Fig. 1. С0 is an initial sate at the moment of ignition, Сi is a sate at the time moment ti. The transition from the state Сi to the sate Сi+1 is realized using the fire propagation model. At that, each state Сi is described by the set of the values of the object parameters at the time moment ti.

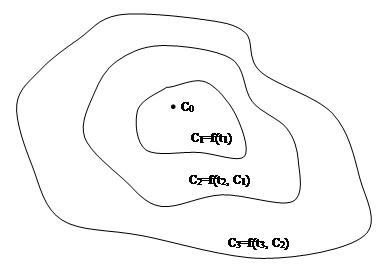
Fig.1. Fire scenario

The object parameters describing the system state are the conditional impact probability eij, the individual impact probability kij, the individual impact dij. In other words, the object parameters are the values from the appropriate cells of the risk matrix (table 1), that is the risk matrix describes the system state Сi at the time moment ti. The variables describing object parameters depend on the initial data.

Each scenario is a sequence of states. The initial state is the moment of ignition at the definite forest area. The probability of ignition is described by the formula (1).

The initial data from the set (11) contain a set of variables that don’t depend on the object parameters. These are the values describing forest plants, meteorological conditions, topography, location and number of fire fighting resources, man's impact.

Alternative is a set of variables describing one of the possible solutions to fire fighting. The choice of the alternative depends on initial data and on object parameters.

Situation Si is an estimation of the set of the values of the system parameters and the relations between them at the time moment ti: , where is the estimation of the system state (parameter values) at the time moment ti, Li is the set of relations between factors known at the time moment ti [13].

The relations between factors can be constant and causal relations that depend on the events and processes occurring. They are stored in the knowledge base (KB) [13].

A situation differs from a state in that it reflects relations between factors and the values of the quality parameters. A situation always represents some estimation (analysis, generalization) of a set of data. This estimation is subjective because it depends on the generalization methods of a certain decision-maker [13].

We have to classify the situations. To do this, we need to determine the indexes according to which each situation will be assigned to a particular class. The indexes will be calculated using the object parameters. According to a class of situation, we have to create the fire fighting plan. In other words, the state Сi at the time moment ti is described by the set of the values of the object parameter and reflected to the set of parameters Zi. These parameters are reflected to the situation Si (12).

Сi → Zi → Si, (12)

Let the fire risk (10) represented as the matrix (table 1) be the index.

Classify the situations depending on the index as non dangerous, potentially dangerous and dangerous.

The hybrid model. For transition from the state Сi to the state Сi+1 (Fig.1) and calculation of object parameters we use analytical models. Let us denote the model of fire danger estimation as Md, the fire dynamic model as Mf, the model of fire risk estimation as Mr, the model of fire damage estimation as Mi. For the calculation of the object parameters we calculate the fire danger at the time moment t0 using the fire danger model:

, (13)

Then, we calculate the parameters of each ith object (the system state) at the time moments t = 1, …, T with the help of appropriate models (14-16):

, (14)

, (15)

. (16)

Finely, we determine the fire risk index which allows to assign the situation to a certain class.

. (17)

Such classification of the situations enables to choose the most rational strategy to influence the situation. Getting a wide range of variants of the situation development allows to reveal critical situations for decision making and possible consequences of the proposed decisions in order to compare them and choose the most efficient [13].

The system architecture is depicted in figure 2.

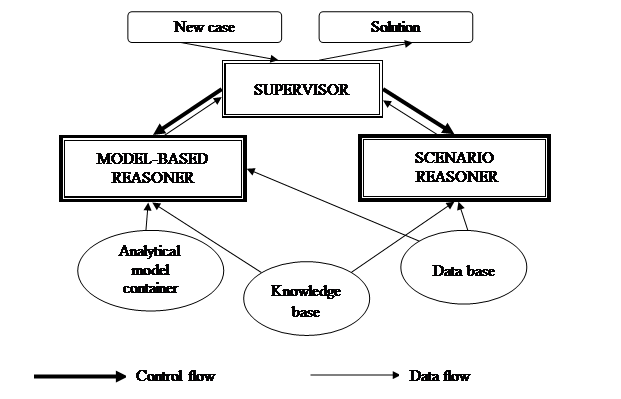
Figure 2. The system architecture

The selection of the appropriate model from the set {Md, Mf, Mr, Mi} is implemented in the model-based reasoner. The models are located in the analytical model container. The building of the fire scenarios is implemented in the scenario reasoner. Data basу contains characteristics of the forest, topography, meteorological conditions, fire statistics. Knowledge base contains causal relations describing the data domain in the form of predicates.

Conclusion. The hybrid scenario-model based approach to the creation of the forest fire protection system. This system represents a new class of intellectual decision support systems namely scenario-model-based decision support systems. The resulting hybrid model enables the development of intellectual systems suitable for work in conditions of incomplete information and uncertainty in complex dynamic data domains. The approach described in the article can be applied for forest fire protection but also in other data domains connected with complex dynamic processes. As a further development of the model we are going to add case-based reasoning which allows to search solutions in new situation by adapting solutions that have been used previously in similar situations. GDSS based on hybrid scenario-model approach may using with remote sensing data of forest fires [17,18].

2. Khodakov V. E, Zharikova M.V. Forest fires: research methods. Kherson: Grin D.S., [Lesnye pozhary: metody issledovaniya. Kherson: Grin D.S.] 2012. 456 P.

3. Raevneva E.V., Berest M.N. Cognitive modelling as management instrument of semistructured systems (situations) [Kognitivnoe modelirovanie kak infstrument upravleniya slabostrukturirovannymi sistemami (situatsiyami)] // Business-inform - Biznes-inform. 2010. N 5 (2). P. 40-43.

4. Luger J. Artificial intelligence: strategy and methods of the decision of challenges, 4 edition. Publishing house "Williams", [Iskusstvennyy intellekt: strategii i metody resheniya slozhnykh problem, 4-e izdanie.: Per. s angl. M.: Izdatelskiy dom «Vilyams»] 2003. 864 P.

5. Merida-Campos C., Rollon E. CBR and MBR techniques: review for an application in the emergencies domain // Universitat Politechnica de Catalunya, (UPC) LSI Technical Report. LSI-03-36-R. 2000. 97 p.

6. Grishin A.M. Mathematical modelling of forest fires and new ways of fighting them. Novosibirsk: Science. Siberian branch [Matematicheskoe modelirovanie lesnykh pozharov i novye sposoby borby s nimi. Novosibirsk: Nauka. Sibirskoe otdelenie], 1992. 408 P.

7. Baranovskiy N.V., Kuznetsov G.V. Concrete of the unstated reasons in a deterministic-probabilistic forecasting model of forest fire danger [Konkretizatsiya neustanovlennykh prichin v determinirovanno-veroyatnostnoy modeli prognoza lesnoy pozharnoy opasnosti] // Fire and Explosion Safety - Pozharovzryvobezopasnost. 2011. Vol. 20, № 6. P. 24 - 27.

8. Bachmann, A. GIS-based Wildland Fire Risk Analysis: Thesis (doctoral) Mathematics. - Zurich, Universidad de Zurich, 2001. 143 p.

9. Torasso P., Portinale L. Combining experimental knowledge and model-based reasoning for diagnostic problem solving // Knowledge-Based Systems: Advanced Concepts, Techniques and Applications. 1997. P. 375-398.

10. Comes M. Decision maps for distributed scenario-based multi-criteria decision support: Dissertation. Kalshure, 2011. 343 p.

11. Nazarov A.A., Terpugov A.F. Probability theory and stochastic processes: Manual. Tomsk: Publishing house NTL. [Teoriya veroyatnostey i sluchaynykh protsessov: Uchebnoe posobie. Tomsk: Izd-vo NTL] 2006. 204 P.

12. Grishin A.M., Baranovskij N.V. Comparative Analysis of Simple Models of Drying of the Forest Combustibles, Including the Data of Experiments and Natural Observations // Journal of Engineering Physics and Thermophysics. 2003. V. 76 N 5. P. 166 – 169.

13. Sherstuk V.G. Formal model of hybrid scenariocase DSS / Automatics. Automation. Electrotechnical complexes and systems, Issue 1, [Formalnaya model gibridnoy stsenarno-pretsedentnoy SPPR / Avtomatika. Avtomatizatsiya. Elektrotekhnicheskie kompleksy i sistemy, Vyp.1] 2004. P. 114-122.

14. Gusev V.G, Korchunova I.Yu. About a method of calculation of speed of distribution of a forest local fire // Forest fires and fighting them. L.: LenNIILH [O metode rascheta skorosti rasprostraneniya lesnogo nizovogo pozhara // Lesnye pozhary i borba s nimi. L.: LenNIILKh], 1986. P. 31-50.

15. Dorrer G.A. Mathematical models of forest fires dynamics. М: Forest industry [Matematicheskie modeli dinamiki lesnykh pozharov. M.: Lesnaya promyshlennost] 1979, 161 P.

16. Chermack T.J. Improving decision-making with scenario planning // Futures. 2004. N36 (3). P. 295-309.

17. Kuznetsov G.V., Baranovskiy N.V. Forecast of forest fires occurrence and their ecological consequences. Novosibirsk: Publishing house of the Siberian Branch of the Russian Academy of Science [Prognoz vozniknoveniya lesnykh pozharov i ikh ekologicheskikh posledstviy. Novosibirsk: Izd-vo SO RAN], 2009. 301 P.

18. Kuznetsov G.V., Baranovskiy N.V. Focused sun's rays and forest fire danger: new concept // Proceedings of SPIE. Vol. 8890, paper 889011; doi:10.1117/12.2033929