1.Introduction.  Classes .  Let  be weighted Hardy space of all functions   of complex variable , which are analytic in a circle of  , and for which

 and

Here  is fixed function from the class of  measurable on   and -periodic functions.

      It is said that any function   from this  class belongs to weight space , if

,  .

The case of Lebesque spaces  we have  for ; in particular, .        Denote

                      ,

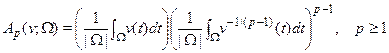where   is arbitrary interval,  and  multiplier is equal  for  by definition.  It is said that   -condition of Muckenhoupt ([1]) is satisfied  and apply the notation  , if  ,. In the present work, as well as in [1], we suppose . Under  this agreement  it can  suppose that everyone  is a function from Hardy class H (the case of  [2], p.431), and if  , then .

              Exclude from consideration a trivial case of  .  Then .  Let E  be a set which is measurable by Lebesque.  Introduce now  the following measure  of Е : .

        Let 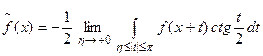 be conjugate function; this function  exists  ([2], p.402)  almost everywhere for .

2. Exponential means of power series and Fourier series (conjugate series).    Let   and  {,    be a sequence of  its  Fourier coefficients.    In various questions of the analysis (see [3]) arises a problem of behavior of  the  families means of Fourier series   

                   ,  ,                       (2.1)

and conjugate Fourier series

           ,           (2.2)

at  .

   Consider now . The  behavior of

                                     =,                                      (2.3)

on boundary of the  circle of convergence (), has been well studied.  So [2, p.432],                                                    exists almost everywhere. Here   and the coefficients  in the expansion (2.3) can be estimated as

                                    , ;                                             

it is natural to assume that  when If we put

                                           ~,                                                     (2.4)

then (2.3) can be considered as a family of Poisson-Abel means of  series (2.4) on boundary of the circle of convergence. Then it will be natural to consider a more general exponential means                          

                    ,                             (2.5)                                           

of series (2.4); the case (2.3) we have for . The following statement establishes a relation  between classes (), (),   () of   the families (2.1), (2.2), (2.5).

 Тheorem 2.1.   If  and , then the representation                                            

()= ())

holds.     In particular (see (2.3)),  =+.

3. The estimates of maximal operators generated  by exponential summation methods.   Let

                                              .                                   (2.6)               Тheorem 3.1.  If ,   then the estimates

;

,  

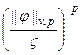hold for every . Here   are constants, which may depend only on indicated indexes.

      This result follows from theorem 3.1 and weighted norm inequalities for maximal operator of the type (2.6), generated by the families of  (2.1), (2.2); these inequalities in the special case of  see in [3].

4. Result of convergence.

Theorem 4.1. Suppose that . Then the relation  =    holds -almost everywhere for each  and in  metric , ,   for any .

      The result follows from the theorem  4.1  and relations     = ,      =, which hold  -almost everywhere for each  and in metrics   ,, for any  

2. Zygmund A. Trigonometric series. Vol. 1. Moscow: “Mir”, 1965. –615 p.

3. Nakhman A. Еxponentially methods of summation of Fourier series. International Journal Of Applied And Fundamental Research. – 2013. – № 2 –URL: www.science-d.com/455-24312 (18.11.2013).