1.      Introduction. Basic definitions and limiting equations.

Suppose    is a real axis,  is a real linear space of n-vectors  x with a norm |x|,  is a real number,  is the Banach space of continuous functions  with a norm ,  is a space .  For a continuous function    and every ,  the function     is defined by the equality  A right-hand derivative is denoted by .

The functional differential equation with a finite delay

                                                      (1)

is considered, where  is a continuous function which satisfies the assumptions 1-3 [1, 2].

2.  Basic results. Stability theorems.

We will investigate the problem of the stability on the base of Lyapunov constant-sign functionals. We shall use the following definitions.

Definition 1. The solution  of Eq.(1) is stable with respect to set , if,  for any   one can get   , so that for   it is true that  for each solution  of Eq.(1) for any .

Definition 2. The solution  of Eq.(1) is uniformly asymptotically stable with respect to set _, if it is stable with respect to  and a  exists, so that for any  one can get  so that for every   it is true that  for any _.

Definition 3. The solution  is a point of uniform attraction for the whole family of limiting equations  with respect to set , if a  exists, so that for any  there is  so that for any solution   of any equation  for any  the inequality  holds.

Suppose  is a certain continuous functional,   is a certain solution of Eq.(1). Along this solution the functional V is a continuous time-dependent function  . For this function it is possible to define an upper right-hand derivative .

Let us denote as  continuous strictly monotonically increasing functions .

Definition 4. Let us define a set for the functional :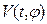

The definitions which have been introduced enable us to derive the sufficient conditions of stability and asymptotic stability when a non-negative functional with a non-positive derivative exists.

Theorem 1. Suppose that:

1)                 a continuous functional  exists, so that ;

2)                 the solution  is a point of uniform attraction for solutions  with respect to the set .

Then the solution  is stable by Lyapunov.

Theorem 2. We will assume that:

1)      the continuous functional  exists such that:

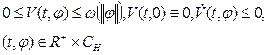
2)      the solution  x=0  is asymptotically stable uniformly with respect to the set  

Then the solution x=0 of equation (1) is uniformly stable by Lyapunov.

3. Conclusion. There is the development of the method of  Lyapunov constant -sign functionals with using of the limit equations in the work. The obtained theorems 1,2 develop and expand some results from [2].

2. PAVLIKOV, S.V., Lyapunov constant- sign functional in the problem of stability of a functional-differential equation. PMM., 2007, 3, 377 – 388.