Setting the problem.

            Let us study stationary equation of Schrödinger with two independent variables that can be formally put in the following expression without physical sense of arguments [3]:

In certain cases while    correct settings of edge problems in certain conditions are found for the mentioned equation .                      

  The presented work studies:

    In area  should be found a solution to equation                                                                                                                                                                 that will satisfy border condition

                                                          (2)

Notice 1.  Further we shall consider circle radius as a unit of scale of the studied system of coordinates R=1 in order to simplify calculations.

Dividing variables according to method of Fourier.

Unconventional solution of border problem 1 will be located in polar coordinates as                                                                                                                                                                            (3)                             As a result of placing product (3) into equation (1) and dividing variables with constant ⅄ we receive equation for the function                                                                                                (4) and problem for proper values for the function                                                                                    (5)         General solution of homogeneous linear equation (5) is defined via characteristic equation, presented as superposition of harmonics                                                                                                        If  is to be single –valued periodic function, the following conditions must be satisfied: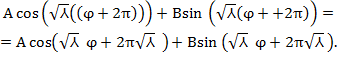

Selecting proper values of ⅄ =  we receive

                                   (6) 

For every fixed value of n of (4) we receive                                                                                                      (7)         Since equation (7) for each given  has a special point while ,  solution of it will be presented as a degree line that starts with    :                             

                            (8)                     

Values of characteristic index  and coefficients of    can be defined via placing line (8) into equation (7). As we consequently equalize coefficients by    to zero, we receive a system of equations:

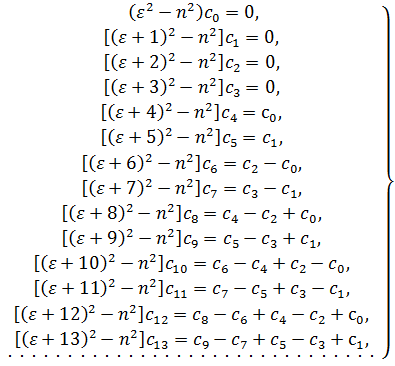
            Considering  from the first equation we find  .                                         

In order to define singular border while  we consider solution of equation (7) as   Then, from the last system we conclude  .  In this case all further odd coefficients of  must also equal zero, and all even coefficients are defined through the sum of previous ones according to alternative formulas

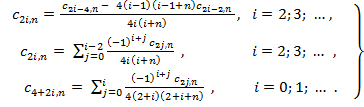                                         (9)

Consequent implementation of formula (9) while    allows us to receive expression                                                                                                       ,

,

     ,

.  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .   .  .  .  .  .  .  .  .

While                  

                                                                      (10)

 Let us designate special auxiliary functions                                                           (11)                            Considering equations of system (10) while    can be expressed as                                                   

,   

,             .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .                                                                                                 (12)                               Example of calculating coefficients of line (8).  

According toformulas (11) - (12) we define coefficients of line (8): a)   and    b)

Solution.  а)              

Let us define value of coefficient :                   

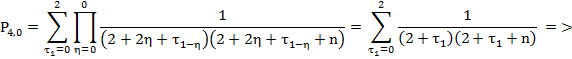
We define    .  Since

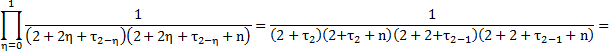
 , we receive

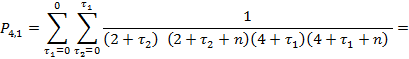
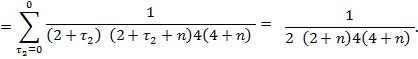
Placing  and   into formula   ,  we receive             

    =     

c) =

.

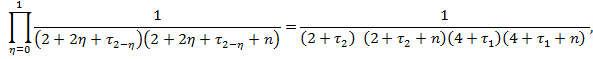
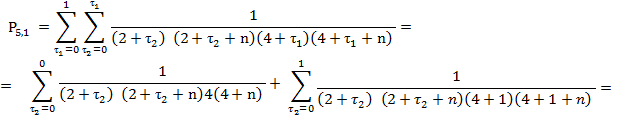
Algorithm of calculating coefficients.    

In order to simplify the process, algorithm of calculating coefficients of line

will be studied at the example of forming multiple sums, presented as

Let u first define consequences of sums  with the same index of                               

While   we receive

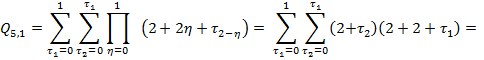
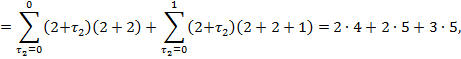
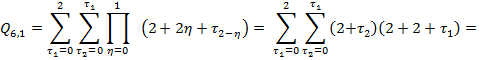
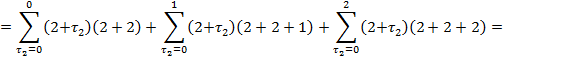
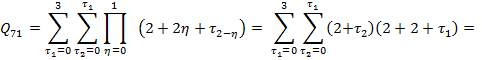
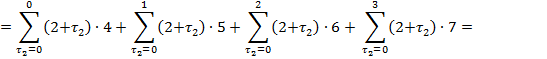
Consequences of multipliers in summands of the studied sums ,   can be easily composed with triangular matrixes

   ,    ,   

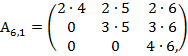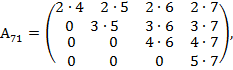
As this trait is possessed by all expressions of , we shall call them multiple multinomials of triangular presentation, and functions that present their modification, will therefore ba named multiple sums of triangular presentation.

  Solution of edge problem 1. Uniting the received results, we define solution of problem (1) - (2) in polar coordinates

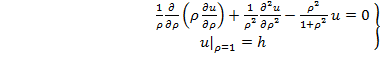                                                      (13)

According to formula  (3):                                                                                                       

Above we have proved that after splitting variables of problem (13) we receive two equations, the first one

                                                                                                                  has proper solutions (6)                                                                                                                   

For each fixed  n  the second equation

                                                                                                     has proper solutions, presented as (8)                                                                                                                            Coefficients of degree line (8)  are defined according to formulas  (12)                                                         ,                                                                                   in which     and multiple multinomials  are defined by correlations (11)                            

 Placing expressions  and into formula (3), we define two systems of proper functions   and   that are met by certain solutions of the first equations (13)                                                                                                                     Superposition of all these solutions                                                                                                         (14)    

Will also be solution of this equation.                                                                                        Coefficients    and    are defined from border condition (13) 

                                          (15)                   if function    is distributed into absolutely and equally convergent trigonometrical line of Fourier

                                    (16)

                                                                                                                       Comparing lines (15) and (16), we receive

                                                    (17)

Applicability of the principle of superposition.

            Convergence of the constructed lines, possibility of their differentiation in circle  and also continuity of function  at the border of this circle are proved via classical methods .                    

            Via alternating method of Schwartz the formed solution can be prolonged outside circle borders into areas of more general view [1].

2. A.N. Tikhonov, A.A. Samarskiy Equations of mathematical physics: textbook / Moscow, Nauka, 1977, 735 p.

3. A.D. Polyanin Reference book on linear equations of mathematical physics / Moscow, PHYSMATLIT, 2001, 576 p.

4. L.S. Sergiyenko Mathematical modeling of physical-technical processes / Irkutsk, Ed. office of Irkutsk state technical university, 2006, 228 p.

5. L.S. Sergiyenko, A.V. Bayenkhayeva On problem of Dirichlet for one class of elliptic equations that degenerate on axis // Modern methods of functions theory and related problems: materials of Voronezh winter mathematical school / Voronezh state university, Moscow state university of M.V. Lomonosov, Mathematical institute of V.A. Steklov of Russian Academy of Science. –Voronezh: editing-printing center of Voronezh state university, 2011. 374 p.

6. L.S. Sergiyenko, A.V. Bayenkhayeva The first edge problem for stationary equation of Schrödinger class // Messenger of Irkutsk state technical university / scientific magazine – Irkutsk, Ed. office of Irkutsk state technical university, 2011, №10, issue 1 (48) – 342 p.

7. Sergiyenko L.S., Nesmeyanov A . A. ON EVOLUTION OF STATIONARY PROCESSES NEAR THE ORIGINS OF EXCITATION // INTERNATIONAL JOURNAL OF APPLIED AND FUNDAMENTAL RESEARCH, «RUSSIAN ACADEMY OF NATURAL HISTORI » «EUROPEAN ACADEMY OF NATURAL HISTORI » : RUSSIAN ACADEMY OF NATURAL HISTORI (Akademiâ estestvosnaniâ) - №1, 2012. - 54 c.