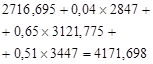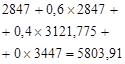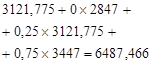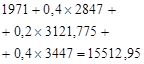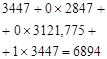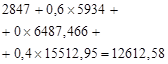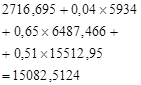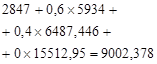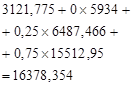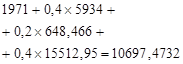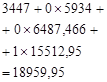Meeting the challenges of constructing models of decision-making remains in the currently weak-formalized area in which the quality of the solutions essentially depends on the experience and intuition of researchers [3]. Currently, there are many different methods of decision making, suitable for solving problems, and at the same time there are practically no formal recommendations on the selection method for a given task. In this context, the aim of this research is to develope a mathematical model based on the Markov model of decision-making.

Businesses wishing to get a loan from the credit institutions (banks), as at the time of the loan may be in one of three states: state 1 - prosperous company, state 2 - the financial condition of the company is such that it is in the "5 years before bankruptcy " state 3 -" a year before the bankruptcy ". It is known from [1] that a company may be in any of this state, if at least three indicators pointing to Beaver belong to this state.

We assume that the decision maker (DM) from the lending institutions (banks) consider two possible options for action (strategy): - to give, - not to give the company credit. We also assume that, depending on the state of the company , , which is consistent, that its generated income can be calculated by the lending institutions (banks). For example, if at time the company was in a state and at time the state continues, it will be considered as the maximum income.

For example if thousnd rub, then the income matrix will be the limit as , where is the matrix elements of transition probabilities .

Assume that we know the statistical (accounting) information of a company for three years . On the basis of these data, we calculate the coefficients , from Beaver and probability [1] , we have that the enterprise under investigationis is in state at time , . For illustrative purposes, the stitistical data for years was taken fro a particilar company OAO «Ленмолоко» [3]. The transition probability matrix is as follows :

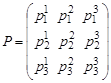; (1)

Elements of the matrix denotes transition probability of the system in state . Thus the rows of the matrix correspond to the "state " and the colums - “time ”. The sum of elements of each row is unity that is , .

For the simulation of the situation in the company, the transition probability matrix may be represented in the income matrix as follows: :

,

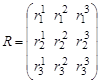element of the matrix denotes the income obtained at time when the system is in state .

With the matrix and one can simply predict the results of the system. In this case, the set of feasible solutions , where - the decision to issue a loan the company, and - not to issue. Thus, the transition probability matrix is given by [4,5]:

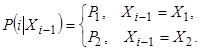
The transition of the company from one state to another is associated revenuematrix whose element is the income (positive values) for the -th stage. At the same time, the income in -th stage is associated with the transition of the company from state , in which it was after the -th stage, a state when deciding whether .

Values [4,5] defines the expected revenue for the -th stage, if after the -th stage the company was able to be in state and it was decided to .

It is necessary to note that the decision-maker may be interested in the value of the expected income at a predetermined strategy of behavior in case of a state company . For example, PMD may consider that after -th stage if the enterprise is in State , regardless of the particular value , it is necessary to make a decision .

For a finite planning horizon, ie, a finite number of steps of Markov decision problem with the principle of optimality, which is to maximize the expected revenue for the stages, it may be represented as a dynamic programming problem.

Let - expected optimal revenue ( that is optimality principle in its best use) for stages with numbers , provided that after the -th stage of the test, the company is able to be state , . Since the planning horizon is finite, then the optimal expected revenue requirements must be satisfied

,

Expected optimal revenue phases numbered consists of two component The first component - optimal revenue for -m stage, due to a transition of the company from a state in which it was at the -th stage, in any admissible state, [2,5]. ; (2), where - the conditional probability that, after the -th stage the company will be in a state and has a feasible solution ; - . income of the company in state , in which it was after the -th stage as a result of , from the set of feasible solutions . The second component of the optimal revenue determined by a combination of optimal income , , with transition probabilities , :

.

We come to the recurrence equation of dynamic programming with a finite number of steps linking the expected optimal revenue , и , , :

, , .

In this case, we recall that , и ,

Example: Assume that the lending institutions (Bank), considers the enterprise in question to provide credit. To do this, the bank needs to develop an optimal behavioral strategy, that is, to maximize the total return for the loan to the entity. Recall that the investigated company has identified three possible states: State 1 - prosperous company, state 2 - the financial condition of the company is such that it is in the "5 years before bankruptcy," state 3 - "a year before the bankruptcy." Set of feasible solutions , where - the decision to issue a loan company, and - not to give. Transition probability matrix has the following form (see. (1)) [5].

This discourse was taken from a known statical (accounting) data on a gravity . On the basis of these data, we calculate the coefficients W. Beaver and probability that the investigated the company is in state at time , , j = 1, 2, 3. Then, the transition probability matrix P₁ is as follows: 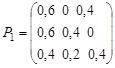. The sum of elements in each row is unity, that is , .

Suppose that on the basis of the resulting matrix of transition probabilities matrix is calculated as follows: : 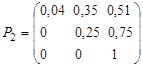, and the income matrix in accordance with the transition probability matrix is calculated by the following formula where th. rub. - desired income at time , and - elements of the matrix of transition probabilities

;

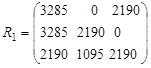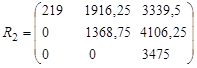
We assume that the planning horizon is . From these matrices , , , , we calculate the expected revenues from the formula (2), due to the transition from one state to another in different variants of feasible solutions of the sets G of the companies considered:

,

,

,

,

,

.

For clarity, we use the tabular algorithm for solving this problem.

Table 1. Calculations of optimal expected revenue for the 1st stage of planning.

Table 2. Calculation of the optimal expected revenue for the second stage of planning.

Table 3. Calculation of the optimal expected revenue for the third stage of planning.

From the results, we conclude that the best solution for the three years (phase) is - not to give credit to the enterprise, regardless of the economic market situation. For all three years (stages) it is optimal to assume as the feasible solution for all the possible states of the enterprise.

2. Nedelko V.M. Some questions evaluating the quality methods for constructing decision functions // Bulletin. that. state. Univ. management, computer sc.& inf.. 2013. №3 (24). p.123-132.

3. The financial statements of the enterprise O.A.O. "Lenmoloko" (2013): [electronic resource] // - Mode of access: URL: http://www.len-moloko.spb.ru/documents/balance.html/.

4. Volkov, I. K., Zagoruiko E. A. operations Research: Textbook / Ed. by C. S. Zarubin, A. P. Grishenko. - M.: Izd-vo MGTU im. N. E. Bauman, 2000. - 436 S.

5. Chernorutskii I. G., Methods of decision-making. - SPb.: BHV-Petersburg, 2005. -416