- The optimum thickness of the coating, providing the main function of protection, and the possibility of variations in the structure (composition);

- The hardness of the surface layer which interacts with the metal;

- The complexity of the protective coating defined number of layers and the number of components in the coating layers.

Accordingly, the factors that determine the service life of molds, will be:

- The thickness of the protective coating, max = 8 um, min = 2 um;

- The hardness of the surface layer, 54-62 HRC;

- Complexity coverage - comprehensive indicator reflecting the number of layers and the number of components in layers: 1 - single-component bilayer; 2 - one-two-two-layer; 3 - three-layer of two or more component.

Correctness chosen above factors was confirmed by experts in the field of injection molding.

To construct a mathematical model is necessary to conduct experiments with the maximum and minimum values of each factor, each experiment must take place no less than three times.

Statistical data on the resistance were selected using the methods of planning experiments. For drawing up the matrix of experiments was involved method of rational design of experiments, which allowed to obtain empirical correlations for multiple correlation with a minimum of experiments. To solve this problem of the possibility of complete or fractional factorial experiments. Since complete factorial experiments allows you to get a more accurate result optimum, then we use it this method to solve the problem.

The analysis was performed in the following sequence:

- Coding of variables;

- addition planning matrix encoded variables into account interactions of factors;

- Calculation of the coefficient of the regression equation;

- Verification of the calculation of coefficients on the importance of pre-determining the reproducibility of the dispersion, and regression equations in coded variables;

- Check on the adequacy of this equation;

- Interpretation of the resulting model;

- Prescription of the regression equation in the natural variables.

The regression equation was obtained in the coded variables:

y(N)=219,04+13,292х1+14,958х2+13,208х3+1,5417х1,2+1,625х1,3-9,292х1,2,3

where y (N) - service durability of parts (in thousands. cycles), x1, x2, x3 - relevant factors х1,2, х1,3, х1,2,3 - interaction factors.

Interaction of factors х2,3 defined as insignificant.

Check the adequacy of this equation is to compare the estimated value of the Fisher criterion  with the tabulated value.

Define the estimated value of the Fisher criterion :

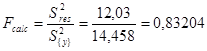
where  - residual dispersion,  - dispersion of reproducibility.

Tabular values  are the critical points of the tables Fischer at a significance level of α = 0,05 corresponding degrees of freedom k1=n-r=8-7=1   and k2 =n(m- 1) =8·2=16.

Since = 0.83204 <= 4.49, the regression equation adequately

An interpretation of the resulting model:

From Equation 1 shows that the greatest impact on the operational stability of the molds has a factor of х2 - the hardness of the surface layer, since it has the largest absolute value ratio.

Further, the strength of influence on the service life of molds follow: х1 - the thickness of the coating, х3 - the complexity of the coverage; interaction of factors х1,2,  х1,3, х1,2,3.

The resulting mathematical model predicts the operational stability of molds for injection molding with a protective coating, as well as to adjust the resource based on the actual surface hardness.