Abstract: In this paper, we provide a very accurate numerical and semi-analytical solution to a system of nonlinear differential equations derived in modeling the effect of bi-therapeutic treatment of tuberculosis (TB) in a homogeneous population consisting of different groups (six different groups). The model studied the outcome of simultaneous application of isoniazid preventive therapy – IPT and antiretroviral therapy – ART in the treatment of TB. The numerical analysis made use of MATHCAD program and the result showed that accelerated control and eradication of TB is predominantly affected by a number of the model’s input parameters such as: proportion of infectious individuals who use only IPT, the proportion of infectious individuals that use only ART, proportion of individuals who use both IPT and ART, the rate at which latently infected becomes infectious and the per capita rate of susceptible becoming latently infected. The model allowed us to evaluate the isolated performance of these treatment factors with ART indicating more active result. Our analysis show that effective eradication of TB can be achieved where a significant number of infected individual are exposed to free bi-therapeutic treatment and situation where this control measure is stipulated as a norm for the treatment and eradication of tuberculosis (TB).

Keywords: bi-therapeutic, isoniazid, antiretroviral, latently, vulnerable, chemotherapy, nosocomial, hypothetically, eradication

1. INTRODUCTION

Tuberculosis (TB) has it history as far back as the seventeenth century, when it was first identified as the major cause of death in Europe, particularly in England [1][2]. Mycobacterium tuberculosis is known to be the causative agent of Tuberculosis disease, (TB) [3][4]. The disease is said to be causing more death worldwide than any other single infectious disease [5, 1, 6].

Following the increase in the reemergence of Tuberculosis in the Sub-Saharan Africa, Asia and Eastern Europe, consequent upon HIV pandemic in the second half of 1980s, World Health Organization (WHO), in 1993 declared tuberculosis, a global emergency with 2 billion people estimated to be infected by TB that year [7, 8, 9]. Other factors considered responsible for the growing TB spread, is the high prevalence of multidrug- resistant strains which was estimated to account for third of the world population infected with TB [10]. The alleged pandemic have no-doubt cause a substantial threat to socio-economic development and imposing a heavy burden on families, communities and the economy of the affected nations [11].

The progression rate of TB to its clinically active disease appear in two folds – the “fast” develop TB, which takes within 2 years to progress to clinically active TB and the “slow” TB, which remain latent and gradually develop to clinically active TB in 20 years [4, 10, 12]. The most vulnerable people are those living in poverty with 70% of the cases occurring among the age group of 15 – 59 years (the most productive age group), whereas, in the developed countries, elderly people are more affected, with nearly 60 – 65% of newly diagnosed cases being males [13][14]. Tuberculosis transmission is by direct contact of the susceptible with aerosolized particles containing live tubercle bacilli released by individuals with infectious tuberculosis disease (Ii), [15][16].

Due to the emergence of drug-resistant TB strains and convergence of HIV and TB epidemic, the control of TB is of paramount importance. The main intervention and control measures comprises of BCG vaccination and the World Health Organization’s “Directly Observed Treatment Short-course” (DOTS) chemotherapy, which involves active case finding, isoniazid prevention therapy (IPT), anti-retroviral therapy (ART) and treatment of patients with multidrug-resistant TB [4, 17, 18, 12, 19, 20].

In the context of TB disease, appreciable number of mathematical models has been widely used in various forms to study the transmission dynamics of TB epidemic. These include models [21][22], that considered drug-resistant TB; [23][24], that considered both co-epidemics of HIV and TB; [25], worked on the Prospects for Worldwide tuberculosis control under the World Health Organization, DOTS strategy; and [26] studied differential equation models of some parasitic infections.

The background of this present study alludes from the model [3]. In that model, application of time-dependent sensitivity and uncertainty analysis were formulated to study tuberculosis model in order to quantitatively understand the transmission dynamics of untreated tuberculosis epidemics. Also, playing a vital role in this paper is the study [10], where the model was on sensitivity analysis of multidrug-resistant TB (MDR-TB). In this paper, we account for the dynamics of the effect of the application of bi-therapeutic (isoniazid preventive therapy – IPT and antiretroviral therapy – ART) treatment of TB infection using compatible mathematical parameters as a wholesome new novelty features. The model incorporate the biology of tuberculosis transmission as presented by each of the six compartments over time, (see fig. 1).

In particular, we performed the simulation analysis using MATHCAD with in-built ‘rkfixed’ function to determine the most influential parameters. This is important in terms of both the application of chemotherapy and refinement of improved models in the context of TB control.

2. PARAMETERS AND MATHEMATICAL MODEL

In formulating this model, we consider the model [3], with which we construct a relatively simple model for a bi-therapeutic treatment of TB, as seen in the differential flow-chart below: (Note: the proportions highlighted are the new novelties of this present model).

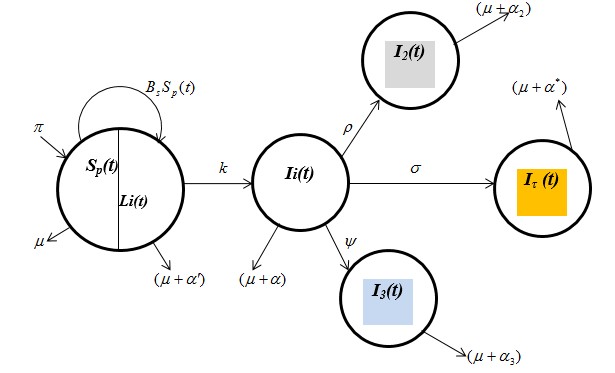
Fig. 1: A differential flow-chart for TB bi-therapy treatment model.

From fig. 1 above, the parameters (functions) prescribed in the model are defined as follows:

Sp(t) - Susceptible population at time t;

Li(t) - Latently infected individuals at time t;

Ii(t) - Infectious individuals at time t;

I2(t) - Infectious individuals who use only IPT at time t;

I3(t) - Infectious individuals who use only ART at time t;

Iτ(t) - Infectious individuals who use both IPT and ART at time t;

Bs - Per capita rate of susceptible becoming latently infected;

K - The rate at which latently infected become infectious at time t;

Np - Total population understudy;

- Proportion of infectious individuals who use only IPT at time t;

- Proportion of infectious individuals who use only ART at time

t;

- Proportion of infectious individuals who use both IPT

and ART at time t;

- Probability of transmission by Li per unit time;

- Probability of transmission by Ii per unit time;

- Probability of transmission by I2 per unit time;

- Probability of transmission by I3 per unit time;

- Probability of transmission by Iτ per unit time;

cs - Average number of contact by Sp with Li

cl - Average number of contact by Li with Ii

ci - Average number of contact by Ii with Sp

Π - Recruitment rate of susceptible, π ≥ 0;

- Natural death rate, ≥ 0;

- TB-related death rate from Ii ,

- TB-related death rate from I2 ,

- TB-related death rate from I3,

- TB-related death rate from Iτ,

- Death - related latent infected of TB is negligible (since, Li(t) are not infectious)

The necessary assumptions of the model are as follows:

- The epidemiological population are either -

(i) Susceptible (at risk of contracting the disease), Sp

(ii) latently infected ( but not infectious), Li

(iii) infective (capable of transmitting the disease), Ii

- Population understudy is heterogeneous.

- Recovered individuals are naturally recruited into the susceptible population.

- Latent infection related death rate is negligible.

- Age structure is ignored.

- Multidrug-resistant TB/HIV is ignored.

- Reinfection does not occur [3].

- Nosocomial transmission (transmission from patients within hospital settings) is ignored.

- Infection and death are not life-span dependent.

- Population is homogeneous.

Induced from fig.1 and the above assumptions, the model is governed by the following derivatives:

(2.1)

(2.2)

(2.3)

(2.4)

(2.5)

(2.6)

The population understudy is defined by the equation

(2.7)

From equations (2.1) and (2.2), the per-capita rate of latent infection denoted by is derived in relation to the individual fractions,, , , of TB – infected individuals [26]:

(2.8)

3. EQUATION TRANSFORMATION AND ANALYSIS

Equation transformation to dimensionless form reduces the number of equations for easy handling and initiates the biological meanings of the proportions of infected individual as well as defines the incidence and prevalence of infection.

Suppose,

Then, in terms of proportion,

(3.1)

(3.2)

(3.3)

(3.4)

(3.5)

(3.6)

Proportion-wise, let p(t) represent the effective population. Then we define as

(3.7)

Applying similar transformation approach, equations (2.1) – (2.6) becomes,

(3.8)

(3.9)

(3.10)

(3.11)

(3.12)

(3.13)

Further, we transform the coefficient of incidence of infection to dimensionless form [27][28], i.e. equation (2.8) become,

(3.14)

The latently infected individuals (Li), do not shed bacilli and are not infective to others. In some latently infected individuals, the infection remains latent and the infection may persist for life [15][19]. Therefore, at latently infected stage, if, then equation (3.8) become,

(3.15)

Therefore, the model is governed by the 6 non-linear differential equations in 6 groups of the populations as highlighted in the summary of Table 1 below:

4. NUMERICAL SIMULATIONS AND RESULTS

Here, we set the 6 differential equations involving the populations () to a number of numerical simulations using a set of hypothetically generated data as highlighted in Table 2 below:

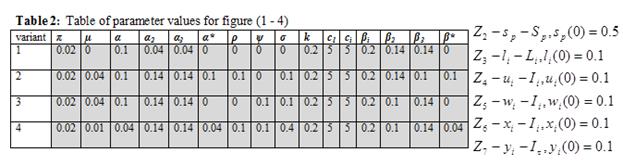
The characteristics of the proportions of the various population understudies are constant and are designated as follows:

P(t) = () = [0.5,0.1,0.1,0.1,0.1,0.1]

and ; .

In order for the parameters to be Runge-Kutter method compactible, we transform the characteristics into vector quantities.

Let

= =.

Therefore, the systems of differential equations can be written as

.

The computation is further enhanced by the use of MATHCAD grogram with in-built “rkfixed” function [29].

In the analysis that follows, we focus on our set goal – the dynamics of the effect of bi-therapy treatment of TB patients which is predominantly determined by. Other parameters were equally tested. Graphically, we represent the time by Z<1> and let Z <2>,……, Z <7> represent respectively with , as seen in figures(2 – 5), below:

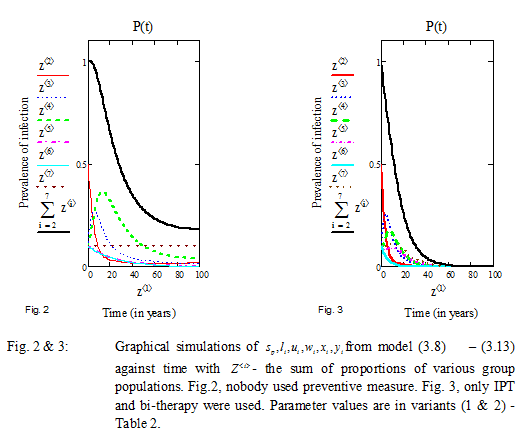
From figure 2 below, we investigate the zero variant factors (i.e. ). Here, with 20% rate of latently infected becoming infectious (i.e.) and in a situation where nobody uses the bi-therapeutic treatment, as expressed in variant 1,we observed that the population experienced an initial rapid infection due to high average contact rate. The susceptible population is engulfed by infection after 20 years. Infection at various proportions decline but persisted steadily after 40 years due to overall transmission rate which stood at 14%.

Under figure 3 below, we study the performance of the bi-therapeutic treatment, allowing the parameters as in fig. 2, with only variations in factors i.e. . It is seen that TB transmission was rapid, consuming the entire population within 30 – 50 years interval. This can be attributed to the fact that, zero proportion uses the ART and only 10% were exposed to IPT and bi-therapeutic treatment.

In figure 4 below, the effect of the bi-therapies was further analyzed by the enhancement of the parameters of figure 3, increasing the proportion of infectious individuals that use the ART by 10% while the proportion that uses the IPT was allow to remain at zero. With 10% proportion of the individuals that use the bi-therapies (both IPT and ART) and zero transmission by this group, simulation indicates low and slow transmission of infection, compared to fig.3. It is arguably noticed, that the ART is more effective compared to the IPT, as shown by against. The entire population were consumed by the infection but sustained by the introduction of bi-therapeutic treatment.

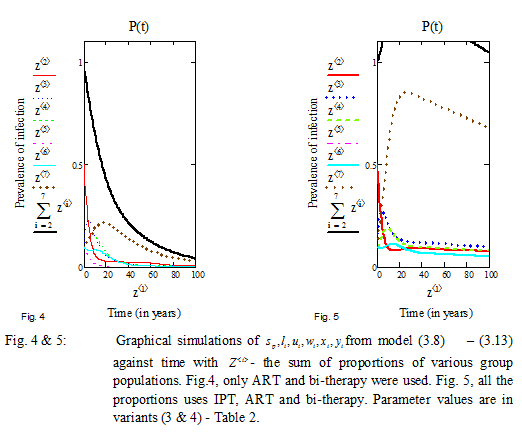
Finally, as in figure 5 above, we attempt and visibly analyze the effect of the bi-therapeutic treatment by absorbing the parameters as in fig. 4, but with an enhancement of the proportion of the individuals who use both IPT and ART simultaneously by 40% (i.e.), accounting for low transmission rate as well as related death rate of 4%. We observed initial rapid infection in the early 30 years, but were curtailed by the application of IPT and ART respectively. Figure 5, indicates that with the combination of both IPT and ART simultaneously, infected population generally have greater chances of surviving and living longer live even after 100 years with lesser probability of transmitting the disease.

5. DISCUSSION

In the paper, we present the dynamics of the effect of bi-therapeutic treatment of TB epidemic, an investigation informed by the work of [3]. That study was basically on the understanding of the historical epidemiology of tuberculosis in developing countries where treatment is not a norm. Therefore, this present work which account for the effect of treatment of TB infection, justify its relevance. The model was instrumentally constructed using 6 groups of the population which leads to 6 non-linear differential equations. It also took onto account, natural birth rate which include recruitment of recovered individuals; and related death rate from the considered groups of infected population.

Our model allows incisive comparison of the independent performance of treatment factors (i.e. IPT and ART) and as well, the combination of both factors simultaneously in the fight to reduce and possibly eradicate the spread of TB disease. From the studies, we observed that the general behavior of these treatments depends predominantly on parameters such as ,.

In our program, we use MATHCAD, with rkfixed in-built Runge-Kutter function. Results obtained from the numerical simulations of the model equations indicate that both therapies are vital in the treatment of TB infection. However, as a single treatment, ART have shown to be more active compared with IPT. The investigation further reveal that prolonging the lives of the infected individuals and eradicating the spread of the disease, is best control with through simultaneous application of both IPT and ART to affected patients. Figure 4, clearly vindicate this situation.

6. CONCLUSION

Investigation on the individual performance of IPT and ART and as a combined factor for the treatment of TB has been successfully conducted. The numerical analysis suggests that despite the individual effect of IPT and ART respectively on the control and treatment of TB, the study have recommended the use of bi-therapeutic treatment as a norm for accelerated control and eradication of the spread of TB among infected individuals and the society. The result shows that for effective eradication of TB disease, adequate provision of medication should be made available and free to infected individuals. An environment of highly significant application and adherent to treatment will enhance the set goal of complete eradication of TB. The study also recommends continuous awareness campaign and education of the public, especially the developing countries on this best treatment measures.