We consider the problem on numerical simulation of the longitudinal, transverse and surface waves on the free surface of an elastic half-plane under concentrated impact in the form of Delta functions and Heaviside functions. For the solution of two-dimensional non-stationary dynamic problem of elasticity theory with initial and boundary conditions we use the method of finite elements in displacements. The problem is solved by the method of end-to-end account, without allocation of breaks. Solve the system of equations of 48032004 unknown. Shows the variation of elastic contour stress on the free surface of the half-plane. The amplitude of surface waves Rayleigh is significantly larger than the amplitudes of the longitudinal, transverse and other waves.

In the works [1–6] gives some information on the practical implementation of numerical modeling of non-stationary of stress waves in complex deformable objects using numerical method, algorithm and software.

In an elastic halfplane from a concentrated impact is subject to longitudinal, transverse, Rayleigh and conical waves. They propagate with different speeds.

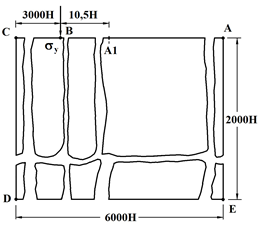
Fig. 1. The problem statement focused on the impact of normal stress on the free surface of an elastic half-plane

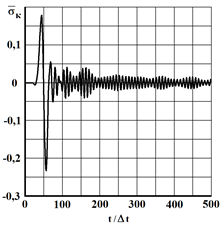
Fig. 2. The change of elastic contour stress in time at the point when exposed in the form of Delta functions

Consider the problem of the influence of focused waves in the form of a Delta function perpendicular to the free surface of an elastic half-plane (fig. 1).

At the point perpendicular to the free surface attached elastic normal stress (fig. 1), which, when varies linearly from to , and when from to (, MPa). The boundary conditions for the contour when . The reflected waves from the contour do not reach to the point when . Contour free from loading, besides the point , where is applied a concentrated elastic normal stress .

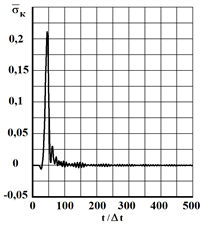
Fig. 3. The change of elastic contour stress in time at the point when exposed in the form of Heaviside functions

The calculations were conducted with the following initial data: ; = 1,393×10^-6 s; = 3,15×10⁴ MPa; = 0,2; = 0,255×10⁴ kg/m3; = 3587 m/s; = 2269 m/s. In fig. 2 shows the variation of elastic contour stress () in time at the point (fig. 1), located on the free surface of an elastic half-plane.

Consider the problem of the influence of focused waves as a function of Heaviside is perpendicular to the free surface of an elastic half-plane (fig. 1). At the point perpendicular to the free surface attached elastic normal stress , which, when changes to , and when anyway (, MPa). The boundary conditions for the contour when . The reflected waves from the contour do not reach to the point when . Contour free of loads, besides the point , where is applied a concentrated elastic normal stress . The calculations were conducted with the following initial data: ; = 1,393×10^-6 s; = 3,15×10⁴ MPa; = 0,2; = 0,255×10⁴ kg/m3; = 3587 m/s; = 2269 m/s. For example, in fig. 3 shows the change of elastic contour stress () in time at the point , located on the free surface of an elastic half-plane.

2. Musayev V. K. Modeling of non-stationary of stress waves in solid deformable bodies complex area // International Journal Of Applied And Fundamental Research. – 2014. – № 2; URL: www.science-sd.com/457-24639.

3. Musayev V. K. Simulation of transient elastic stress waves in a deformable fields using the finite element method in displacements // Modern high technologies. – 2014. – № 12 (1). – P. 28–32.

4. Musayev V. K. Mathematical modeling of surface stress waves in the problem of a lamb when exposed to a Delta function // international journal of applied and fundamental research. – 2015. – № 2 (part 1). – P. 25–30.

5. Musayev V. K. Modeling of non-stationary of stress waves in the shell with an elastic half-plane under the influence of air shock waves // International Journal Of Applied And Fundamental Research. – 2015. – № 2 URL: www.science-sd.com/461-24853.

6. Musayev V. K. Mathematical modeling of surface stress waves in the problem of a lamb when exposed in the form of Heaviside functions // international journal of applied and fundamental research. – 2015. – № 5 (part 1). – P. 38–41.