Active and purposeful use of vibrational effects as a controlling factor is very perspective direction of vibrational technology connected with processing of the disperse systems of viscous-suspension type. It is of great significance to investigate the possible forms of relative motion and dynamic balance of separate phases in multiphase medium under periodic influences such as low-frequency vibrations.

In many cases the vibration does not change the essence of technological processes, but it executes a role of peculiar catalyst considerably increasing process productivity, intensity, or product yield. These processes are performed by means of other driving forces of vibrationless nature: temperature gradients, gravitational and molecular interactions, chemical reactions and others. Vibration field imposing onto such processes permits strengthening or relaxing of vibrationless forces and by that makes it possible to control the technological processes. In such cases the selectivity and the directivity of vibration-field action create opportunities for new highly effective technologies and processes [1].

In spite of the fact that nowadays the acoustic methods of influence on food disperse systems arc being spread wider and wider in various branches of industries, the selection of conditions of acoustic efects on processes are nevertheless based on an empirical approach. Such approach to application of the acoustic effects on chemical-technology processes, which are distinguised by a significant complexity and frequently represented by the combination of chemical, hydrodynamical, diffusional, and thermal processes, does not promote a correct choice of technoilogical conditions, gives no possiblity to optimize them and, therefore, to increase the economic efficiency of processes [2].

2.       EXPERIMENTAL PROCEDURE

Recently the interest in researches devoted to the vibrational methods of intensification of heat and mass transfer processes in beet-sugar production continues to grow. Positive influence of low- frequency acoustic field on crystallizing sugar massecuites as well is being substantiated. And the stated considerations about the mechanism of oscillation influence on the mass transfer are based on hypotheses of the effect on a boundary layer and do not contain quantitative relations.

At the same time, die question of estimation of an existing sugar-crystal boundary layer is a matter of principale, because it allows to determine the efficiency of interactions between phases. Conformably to saccharose they more oten operate with the general concept of boundary layer without considering die hydrodynamic and diffusinal layers' relationship. Such approach is not correct enough.

A laboratory batch vacuum pan crystallizer with vibrostirring mechanism /3/ shown in Fig. I was used for carrying out the researches on isobaric vacuum massecuite boiling with acoustic effects on the crystallizing slurry.

The apparatus involved a cylindrical vacuum-pan case [1] of 0.22m diameter, supplied with an ellipsoidal bottom [3] haveing four boiling tubes [4] of 0.029m diameter with electric heaters of 1200 W total power [5]. The vacuum pan is supplied with a condensator [2]. The branch pipe [6] served for initial filling of the vacuum pan witii a starting product (9-10 dm3 initial charge's volume) and for feeding during boiling. The central channel [7] of 0.06 m diameter provided the descending natural circulation of the massecuite which probes were taken out through a sampler [8]. A vibrostirring element was represented by a disk [9] of 0.076 m diameter punched by conoidal channels, with narrow holes downwards. The channels was of 90° taper angle and of 0.005 m smaller diameter, the disk was of 0.005 m smaller diameter, the disk was of 0.005 m thickness and of 7.8% free cross-sectional area. The disk [9] was fastened to a rod [10], which had a hermetic outlet from the vacuum pan by means of bellows [11].

Vibrostirring of crystallizing solutions by hermonic oscillations was put into practice by an electromechanical vibroexciter constructed with an electric drive [12], which was a thyristor DC apparatus with smooth rotation frequency regulation of an electric motor [14] within the limits of 60-3000 rpm. The output shaft of the electric motor was connected by means of elastic coupling [15] with the shaft [16] of an eccentric mechanism transforming its rotary motion to reciprocating one of the rod [10]. A driving faceplate [17] and a driven one [18] were used as a crank. The radial displacement of the driven faceplate permitted to set the eccentricity value (oscillation amplitude) from 0 up to 0.007 m. The driven faceplate had a pin [19] with a rolling beating [20]. Electric motor parameters by current and coltage being monitored with measuring devices [13].

The parameters of vibration were evaluated by measurement of oscillation frequency and amplitude. The frequency above 4.2 Hz was determined with the elative error of 0.5%, lighting up the vibromechanism with a pulsing lamp [21] of a stroboscopic tachometer [22] combined with a frequencymeter [23].

Before swithcing on the vibratory drive, the amplitude of oscillations was measured from the shaft [16] and pin [19] eccentricity within the accuracy of 0.1 mm, making use of vernier callipers. Practically, the eccentricity measurement was executed by measurement of the displacement of faceplates [17] and [18] relatively to each other in a radial direction.

A crystallizing solution temperature being measured with a mercury thermometer [35] accurate within 0.5°C and the temperature of secondary steam was measured with a resistance copper thermometer [36], which was connected to an automatic bridge with diagram-tape temperature recording within the range of 0-100°C to the accuracy of 0.5°C.

The effective viscosity of crystal slurry was monitored by a measuring converter [26] connected to a vibrational low-frequency viscosimeter [27] with a digital display device [28].

The mass fraction of solids in solution was determined with a refractometer [38] after the crystalline- phase recovery in a centrifuge [37].

In the researches carried out, the batch boiling of high- and low-grade sugar massecuites (A- and C-types) of diferent purity under the vibrostirring by infrasonic harmonic oscillations (the frequency f = 10-12.5 Hz) with the amplitude A = 3 mm was studied. The estimation of the vibration effect was performed with the power of oscillations, initiated in massecuites by the vibratory element, on the bassis of the vibrostirring intensity J = A2f3 (Table 1).

3. RESULTS AND DISCUSSION

The obtained experimental results have allowed to calculate the thickness of hydrodynamic and diffusional boundary layers for saccharose crystals. The calculations have an approximate changes of hydrodynamic and mass transfer parameters in the experiments on isobaric vcuum pan boiling of high- and low-grade sugar massecuites with vibrostirring character, because theestimates of anorder of the derivatives included in the convective-diffusion equation and the Navier-Stokes one are used.

The equations of liquid movement in a boudary layer admit essential simplification, and the flow may be considered to be flat on a reasonably small part of a crystal because of small boundary-layer thickness.

On the basis of consideration of the convective-diffusion equation for the steady-state mass transfer process in two-dimensional liquid flow the following expression /5/ has been obtained:

                                        (1)

where vx and vy are the components of a liquid flow velocity vector on coordinates x and у along the crystal surface and perpendicularly to it, m/s; C is the relative mass of saccharose in the solution, kg/(kgH20); Ф is the shape factor of saccharose crystals (Ф ~ 0.704); dk is the crystal size, m; dd is the diffusional boundary-layer thickness, m; D is the molecular-diffusion coeficient, m2/s.

Table-1. Change in the hydrodynamic and mass transfer parameters during boiling of sugar massecuites combined with mixing induced by mechanical vibrations

As far as the velocity vx accepts a value close to v on the outer boundary of the hydrodynamic boundary layer of the thickness dh, it may be written:

d /dh ~ vx /v ,                                                                      (2)

where d is the distance from the crystal ace, m.

For the hydrodynamic boundary layer the following relationship may be used

,                                                              (3)

where Re0 the local-oscillatory Reynolds number is defined by

Re0 = 4AfФdkr/m,                                                              (4)

where the mean velocity of oscillatory motion of the disk or the crystal w = 4Af; r is the fluid dencity, kg/m3; m is the dynamic viscosity, Pa×s.

Taking into account the small value of Re0 during the saccharose crystallization experiments (Re0<2), it can be concluded from Eq.(3) that the hydrodynamic boudary layer dh is commensurable with the size of crystals and that the solution flow around crystals is laminar.

Substituting Eq.(2) into Eq.(l) and noticing that the first two terms in Eq.(l) are of the same order, one has

                                         (5)

It can be found from Eq.(3) that

                                                      (6)

where v is the kinematic viscosity, m2/s.

Substituting Eq.(6) into Eq.(5), after simple transformations, noticing that d = dd on the boudary of a difftisional layer, one obtains

                                          (7)

where Sc is the schmidt number (Sc=m/rD).

Because of the awkwardness of the analytical solution of Eq.(7), it was solved by use of numerical procedures. Previously for solving this equation, the estimation of hydrodynamic boundary- layer dh thickness was found using Eq.(3).

The results of calculation of the hydrodynamic and diffusional boundary layer thickness for the mean crystal size d = 6×10-4 m in the experiments on isobaric crystallization of high- and low-grade sugar massecuites are shown in Table 2. Analyzing the results it can be concluded that dh and dd become tens of times as little during the realization of oscillatory crystal motion in comparison to their gravitational precipitation in massecuites /5/. It shows the expediency of developing the methods of acoustic efect on the sugar massecuites. For example, the method of oscillatory- state milk-sugar syrup boiling /6/, sugar massecuites /7/ has been developed, and a new type of apparatus for crystallization with vibrostirring mechanisms has been designed.

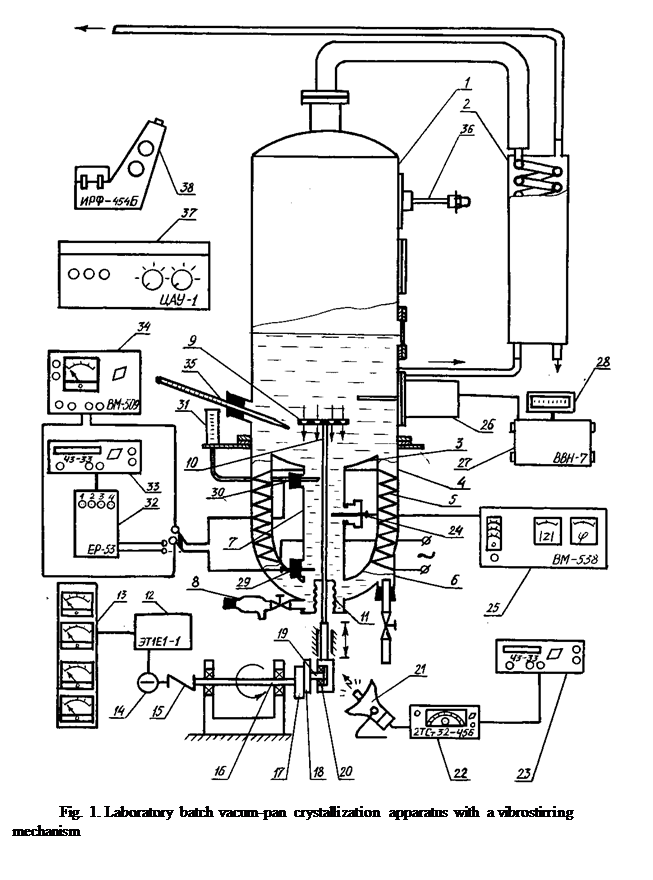
Table-2. Dependence of thickness of hydrodynamic and diflusional doundary layers on the Reynolds and Schmidt numbers during high- and low-grade sugar-massecuite boiling

2. Novickii B.G. Primenenie Akusticheskikh Kolebanii v Khimiko-Technologicheskikh Processakh. Moscow: Khimiya, l983.

3. Petrov S.M. et al. Vestnik of the Russian Academy Agricultural Science. 1994. No. 5. P.56-59.

4. Sheptun V.M. et al. Teor. Osnovy Khim. Tekhnol. 1980. Vol. 14. No. 5. P.764-767.

5. Shestov A.G., Petrov S.M. Izv. VUZov. Pishch. Tekhnologya. l995. No. 3/4. P.46-48.

6. Russ. Patent 2048526, Int. Cl. C 13 К 5/00.

7. Russ. Patent 2155815, Int. Cl. C 13 F 1/02.