INTRODUCTION

In recent years, in the world of science there is an increased interest to the problems of accounting the physical fields effect on real media (liquid, gassy, solid). On the other hand, in the hydrodynamics of fluids there are problems that themselves today, have no rigorous scientific justification. The followings are among such problems:

- in nature there are trees height 100 meters and above. They are called sequoia. There arises a question: what forces rise water in xylems (capillaries) of this tree to the height of 100 m. Theoretical background to this phenomenon has not been found yet.

- A human body includes about 100 km vessels in the form of arteries, viens and capillaries. The characteristic of the blood velocity in the vessels is as follows:

blood the speed of movement of in arteries equals ; the speed of movement of blood in veins equals -; blood the speed of movement of in capillaries equals . The question is: what forces control the movement of blood in the 100 km closed system? What organ of a man executes this function? It is known that a heart is not a pump. Then what moves the blood in the vessels? This phenomenon also has no rigorous scientific background yet.

The fluid in a glass has its certain mechanical characteristics, i.e. density and viscosity. If we place this water in nano-or microtype tube, the fluid will change its properties, i.e. will be different. There arises a question: what kind of mechanism transforms homogeneous fluid into inhomogeneous one in nanotype or microtype tubes? In other words, what phenomenon or unaccounted physical factors transform homogeneous liquid into inhomogeneous one. This problem also remains open.

Tangle of these questions lies in the lack of accounting of hidden physical phenomena in theory of hydromechanics, that hold at the boundary of contact “solid-liquid” in lower-dimensional systems.

Today we have wide experimental investigations in hydromechanics of ideal and viscous liquids in nanostructure system. Variability of mechanical properties (density, viscosity) of fluid in thickness has been shown experimentally, and behavior of fluid on the boundary of contact “a solid- fluid” has been studied.

Simulation of liquid stream through micro and nanotube revealed considerable difference of behavior of fluid in values with sizes about 20 and less molecular diameters from the predictions of classical continual theories. Analysis shows that in a microtube of diameter 50 nm the flow is continuous (continual), while in a microtube of diameter 5 nm the flow is noncontinual, i.e. there is a strong difference in the interaction of fluid-paries in the interval of 5-50 nm.

For describing experimental data of Jirar (O. Darrigol, 2002) in the frams of classical hydrodynamics of continuum, Navier (Navier C.L.M.H. 1823) wrote a boundary condition that taking into account the slippage of fluid along the solid surface.

According to Navier, the velocity of liquid’s slippage on the boundary is proportional to velocity gradient on the paries. The investigations of Kalra and Holt (A. Kalra et al, 2003; J.K.Holt et al, 2006) established that very great slippages hold on nanotubes. And the velocity of the fluid flow is higher by three order, i.e. . The results of molecular dynamical simulation of unsteady mixtures are represented in the papers of Kotsalis E.M., A.A. Evstrapov, S. Abdullayeva and F. Nagiev (E.M. Kotsalis et al, 2004; А.А. Evstrapov, 2001; S. Abdullayeva, F. Nagiyev, 2011). The slippage effects of different fluids on the surface of a nanotube were studied. In the paper of Hongrefi and others (Hongrefi Ye et al, 2011.) it is established that when the liquid particles flow, it is formed an empty layer between the liquid and nanotube. Because of Van der Waals forces of repulsion of heterogeneous particles of carbon and water, the area near the paries of the carbonaceous nanotube becomes inaccessible for fluid molecules. Herewith, the thickness of empty layers independently of the radii of nanotubes practically are the same and equals . Thus, the flow of fluid with slippage becomes more and more important for hydrodynamic problems in lower-dimensional tubes (nanotubes).

Another important phenomenon in a lower-dimnsional system (in a nanotype system) is transformation of homogeneous fluid to structural of inhomogeeous one (E.M. Kotsalis et al, 2004; Hi Chen et al, 2008; Li T.D. et al, 2007;

Semwogerere D. et al, 2007; John A. Thomas et al, 2010; Majumder M. et al, 2010). It is experimentally established that the fluid density and viscosity in lower-dimensional systems change in depth of nanotube and transforms the fluid to structurally-inhomogeneous medium. However, the cause of such phenomena remains open. In other words, what motivates homogeneous fluid to change it mechanical properties, i.e. to be transformed to structurally inhomogeneous fluid: and also what forces provide full slippage of fluid on the of boundary contact with aa solid, remains as an open issue.

THEORETICAL BACKGROUND

The goal of the paper to reveal the mechanism (cause) of appearance of such phenomena that are as follows:

- firstly, in revealing the mechanism of parietal physical phenomenon (physical field), holding between a solid and fluid in lower-dimensional (nanotype) systems;

- secondly, in establishing determining equations of hydrodinamics of ideal fluid with regard to the factor of parietal physical field effect in nanotype systems.

Thirdly, on concrete examples to show the quantity and quality effect of paiertal physical field phenomenon on hydrodynamics of ideal fluid in lower-dimensional (nanotype) systems.

Definition of low dimension of systems. Under the low dimension (nanotype) system we assume mechanical structural elements of nanotubes in the form of capillaries type small diameter tube; the constructions with parallel arranged membranes with a small gap, the constructions of concentrical cylinders with a small gap between the cylinders and so on.

In place of the conditions determining geometrical characteristics of low dimensional systems we take the followings:

1. the lower value of the size of a gap in a low dimensional system should be no less than the diameter of the moleculer of fluid .

This condition is necessary for the fundamental positions of the classic hydrodynamics of fluid be hold,

2. the upper value of the size of the gap in a low dimensional system is chosen as a condition of the existence of parietal phenomenon of electronic field, effect on the fluid property. In other words, effect of arising electronic field on variability of density of fluid in depth of flowing fluid.

Thus, geometrical characteristics for a class of constructions in low dimensional systems will be within:

Here is the thickness of parietal fluid on which the electronic field arising between the solid and fluid acts.

In the numerical form, conditionally the following limit, may be considered as geometrical characteristics of the class of constructions in low dimensional systems: .

The mechanism of formation of physical field in parietal area of solid with fluid. It is known that the atom consists of nucleus and electrons rotating around it. On the surface of a solid the nucleus of the atom is in the solid, and the electrons when they rotate, from one side are in the solid and then they go into the empty space. Thus, when electrons move around the nuclens they are in inhomogeneous space. The part of the space where the electron is in the empty space, forms a physical field called an atomic field. In figure 1 it is shown in the form of domain AC. In the other hand, a part of electrons go out from the solid into the empty space, leave their former orbit and with speed of light move along the tangent to the trajectory that we call the area of electrons radiation. In figure 1 it is shown in the form of area АВ. Thus, on the boundary of the solid it is formed a layer of invisible physical field consisting of atomic field and area of electron radiation (fig. 1).

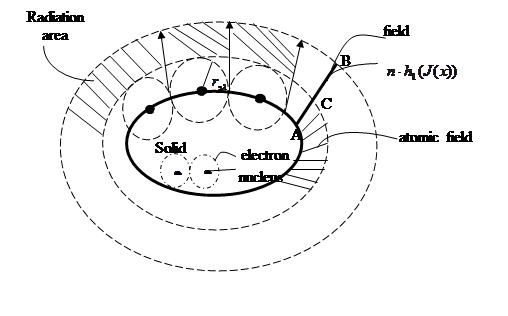
Fig. 1. Geometric representation of formation of physical field on the boundary «a solid-field».

Variability of fluid density depending on variability of tension of electron field in thickness in the parietal area. Let’s consider a tube of diameter in the range in which fluid flows. Under the action of parietal electron field the fluid property will change. And this in its turn will reduce to quantity and quality change of the fluid hydrodynamics (fig.2). It was established that the closer to the paries the nanotube, the density decreases.

Note that mechanism (cause) of transformation of homogeneous fluid into inhomogeneous one, i.e. into dependent on coordinate in radius, remains still open. In other words, what phenomenon or what arising unaccounted forces reduce homogeneous fluid into inhomogeneous one is an open problem.

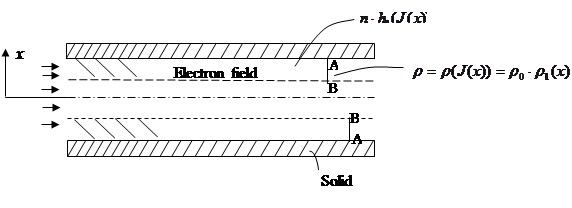
Fig. 2. Form of the fluid flow in electron field in low dimensional systems.

In this connection, the goal of our studies is to reveal the mechanism of relation between the variability of the fluid density on the stress function of the electronic filed changing in thickness. Within the linear variability of the density and electronic field stress in thickness , we suggest this dependence in the form (fig. 3, 4):

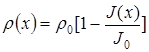, for (1)

where the function is a linear function of the coordinate that varies in the interval 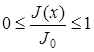for .

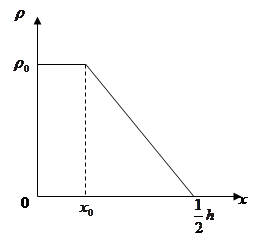
Fig.3. Variability of the density of fluid in the nanotube in thickness .

Thus, under the action of the electronic field arising on the interface of the medium «a solid-liquid», the liquid’s density in thickness changes. And the stress of the electronic field decreases from the boundary of the contact inside. For , , ; for , , .

Taking into account the variability character of the density of fluid in low dimensional systems depending on variability of the parietal electronic field of the form (1), the determining equations of ideal fluid hydromechanics with regard to parietal physical field (electronic field) effect will be as follows:

- the equation of motion:

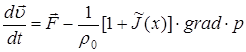(2)

- the equation of conservation of matter (continuity equation):

, for , (3)

- the equation of variability of electronic field in thickness of fluid:

(4)

- the equation of variability of fluid density in thickness with regard to the electronic field effect:

(5)

- the equation of state of fluid (barotropic property of fluid):

(6)

Thus, the determining equations of hydromechanics in low dimensional systems, in particular in nanotubes, with regard to parietal physical field (electronic field) effect phenomenon are reduced to 7 equations with respect to 3 velocity components , initial density , the function of variability of density in thickness, the pressure and the influence function of the physical field stress .

Below, based on the solutions of equations (2)-(6) we will show quality and quantity effect of the influence function of the physical field stress on hydrodynamics of fluid in low dimensional systems.

THEORETICAL FRAMEWORK

Generalization of the Bernoulli equation in low dimensional systems with regard to parietal physical field effect.

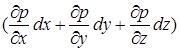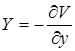Let’s consider the case of steady flow of fluid, i.e. the case . In this case, differential equations of motion of ideal fluid with regard to parietal physical field effect (2) have a solution in the form of integrals under the conditions: if the condition is a total differential of ; secondly, the mass forces have the potential , i.e. , , ; thirdly, if the compressible fluid is barotropic, i.e. .

Under these conditions, we get a so called generalized Bernoulli equation for compressible barotropic fluid with regard to parietal electronic field effect of the form:

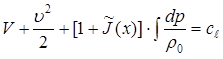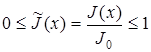, , (7)

This equation holds for all lines of the stream tube passing through the points of the line in thickness situated in the interval .

In the case of incompressible fluid the generalized Bernoulli equation (7) takes the form:

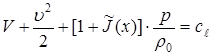(8)

In the case of fluid being under the action of gravity force of potential energy , the Bernoulli integral for the parietal stream line with regard to electron field effect takes the form:

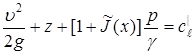, (9)

where 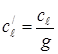is a quantity constant for the stream tube line passing through the point .

Each summand of the left side of formula (9) has a special name and certain sense: the quantity is called geometrical height and determines the distance of the considered particle of fluid from some horizontal plane accepted as a coordinate plane; the quantity is said to be speed height and expresses the height to which would rise the material point if we throw it in a vacuum vertically upwards with initial speed ; we call the quantity 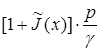piezometric height with regard to parietal electronic field effect that shows what height should have fluid column of stream line passing through the point , for the pressure at its bottom be equal to .

Thus, equation (9) shows that the sum of three mentioned heights has one and the same value at all the points of the given stream line.

Hence, the dependence of pressure on fluid flow velocity will be in the form:

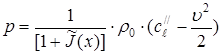. (10)

The equation shows that the greater the velocity of the fluid pressure in the given stream line tube the less pressure is observed at this point, and vice versa, the less the velocity, the greater value has the pressure. Secondly, equation (10) shows that hydrodynamic pressure is always less than hydrostatic pressure that we get if . Thirdly, the dependence of pressure on velocity when passing from one stream line tube to another one with regard to electronic field stress effect changing in thickness, is shown. It is established that the closer the stream line to solid’s paries, the dependence of pressure on velocity decreases and accepts minimal dependence on the paries that is 2 times less than in the case without of electronic field stress stress effect. We give formula (10) in the compact form:

(11)

where , 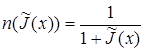. Here for .

It is seen from (11) that pressure and fluid velocity distribution in the cross section will be in the following form. In the domain it will be in the form:

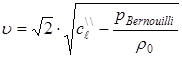, (12)

On the boundary “a solid-fluid”, where for , from formula (11) it will be in the form:

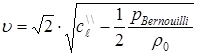, . (13)

This means that the pressure on the stream line near the interface is twice less than the quantity of pressure given by the Bernoulli formula (fig. 5). The velocity of fluid flow near the boundary will be greater than in the domain (fig. 6).

Fig 5. The plot of pressure distribution in depth of fluid with regard to effect of parietal electronic field effect.

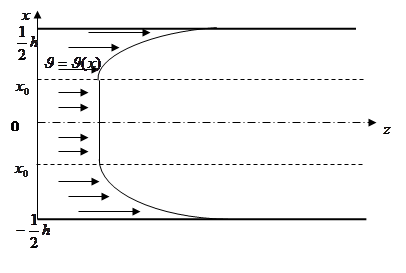
Fig 6. The plot of velocity distribution in depth of fluid with regard to effect of parietal electronic field effect.

RESULTS

In the paper the mechanism of the parietal physical phenomenon holding between a solid and fluid in low dimensional systems is revealed. The parietal physical field is represented in the form of stress of the electronic field 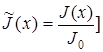; the linear dependence between the fluid density function and the function of variability of the electronic field in depth in the form 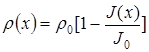is suggested; the determining equations of ideal fluid hydrodynamics with regard to parietal physical field effect in low dimensional systems are constructed in the form (2)-(6); the generalized Bernouilli equation in low dimensional systems with regard to parietal physical field effect was offered in the form (7); the essential quality and quantity effect of parietal physical field phenomenon on ideal fluid hydrodynamics in low dimensional systems was shown.

2. Darrigol O. (2002). Bitween hydrodynamics and elasticity theory: the first five births of the Navier-Stokes equations. Archive for History of Exact Sciences. v, 56, p. 95-150.

3. Kalra A., Garde S. (2003). Hammer G. Osmotic water transport through carbon nanotube arrays. Procedings of the National Academy of Sciences of the USA, v.100, p. 10175-10180.

4. Majumder M., Chorpa N., Andrews R., Yinds B.J. (2005). Nature 2005, 438,44-44.

5. Hongrefi Ye, Yongwu Zhang, Zhongqiang Zhang, Yonggang Zheng (2011). Size and temperature effects on viscosity of water inside carbon nanotubes. Nanoscale Research Letters. p. 6-87, http: //www. nanoscalerelett. com/content/6/1/87.

6. Holt J.K., Park H.G., Wang Y., Stadermann M., Artyukhin A.B., Grigoropoulos C,P., Noy A., Bakajin O. (2006). Fast Mass Transport Through Sub-2nin Carbon Nanotubes. Science, v. 312, p.1034-1037

7. Kotsalis E.M., Walther J.H., Koumoutsakos P. (2004). Multiphase water flow inside carbon nanotubes. Internation Journal of Multiphase Flow, 30, p. 995-1010.

8. Evstrapov A.A. (2001). Course of lectures "Nanotechnologies in ecology and medicine", 136 p.

9. Abdullayeva S., Nagiyev F. (2011). "Nanohydrodynamics". Ministry of communication and information technologies of the Republic of Azerbaijan. Research Center of Higher Technologies. ISBN 5-86874-164-1, Baku, 158 p. (Russian)

10. Hi Chen, Guoxin Cao, Aijie Han, Venkata K. (2008). Punyamurtula, Ling Liu, Patricia J., Li T.D., Gao J. Szoszkiwicz R., Laudman U., Riedo E. (2007). Phys. Rev. B, 75.115415.

11. Semwogerere D., Morris J.F., Weeks E.R. (2007). Fluid Mech., 581, 437-451.

12. John A. Thomas, Alan J.H. VcGaughey. (2010). Ottoleo Kuter-Arnebeck. Pressure-driven water flow throgh carbon nanotubes: Insights from molecular dinamics simulation. International Journal of Thermal Sciences, 49, p. 281-289, jounal homepage: www. Elsevier.com/locate/ijte.

13. Aliyev G.G. (2012). Mechanics of composite materials with changing phisico-chemical properties. "Elm" Puve. House of NAS of Azerbaijan, Baku. ISBN 978-9952-453-13-3, p. 288.

14. Aliyev G.G., Naghiyev F.B. (2013). Engineering Mechanics of Polymeric Materials, (Theories, Properties, and Application). AB?, Apple Academik Press (CPC Press, Taylor & Frencis Croup), New Jersy-Toronto, ISBN: 978-1-926895-55-0, 267 р.

15. Landau L.D., Liphshits. (1944). Continuum Mechanics. Moscow. 524 p. (Russian).

16. Kochin N.F., Kibel I.F., Rose N.V. ( 1948). Theoretical hydromechanics. vol. 2. Moscow, 610 p. (Russian.)