The theory of the differential equations with the deviating argument belongs to number of the relatively young and roughly developing sections of the theory of the ordinary differential equations. There is a number of monographs, entirely or partially devoted to various aspects of this theory. We will specify, first of all, Myshkis A.D. monographs. [1], Elsgoltsa L.E. [2; 3], Krasovsky N. N. [4], Pinni E. [5], Bellman R. and Cook K.L. [6], Norkina of Page B. [7]. The equations with the late argument appear, for example, every time when in the considered physical or technical task force operating on a material point depends on speed or the provision of this point not only at present, but also at some moment preceding this.

For the equation with the deviating argument the considerable number of mathematical works is devoted to creation of the theory of boundary tasks in recent years. Now one of the directions in this theory is developed by Azbelevy N. V. and its pupils [14].

Problem definition.  Let -   the square limited to pieces:

Through  we will designate a set of functions  twice continuously differentiable on  and once continuously differentiable on  in area . The border of area  is understood as set of pieces

We will consider in Hilbert space  the mixed task for the heat conductivity equation:

where

To find Fourier decomposition of the solution of the mixed task (1)-(3).

The purpose - to receive Fourier submissions of solutions of a task (1)-(3).

II. MATERIAL AND METHODS

The regular solution of a task (1)-(3) we will call the function  turning into identity the equation (1) and regional conditions (2)-(3).

We will call function  the strong solution of a task if there is a sequence of functions  and meeting regional statements of the problem such  and , as meets in  respectively to  and  at .

The regional task (1)-(3) is called strongly solvable if the strong solution of a task exists for any right part  and only.[1-5]

In work methods of the complex analysis, theory of operators, theories of the differential equations, the spectral theory of differential operators and the theory of regular expansions are used.

III. RESULTS

Through  we will designate the operator determined by a formula

In space , it is obvious that  the self-conjugate and unitary operator meeting a condition , where  - the single operator.

Affecting with the operator  both members of equation (1), we have

.

Now we investigate spectral properties of the operator . For this purpose we will consider a spectral task:

We look for the solution of this task in a look:

.

Having substituted this expression in the equation (4), we will receive

,

,

.

Therefore,

,

.

from where  and .

For functions  we will receive an infinite series of spectral tasks:

.

Thus, at everyone fixed values  it is necessary to solve a spectral problem:

We will consider more general task:

where  - any complex (generally speaking) constant, and  spectral parameter.

          Having differentiated the equation and having used a boundary condition (6), we will receive a problem of Storm-Liouville:

,

If function  is own function of a regional task (6), it is also own function for a problem of Storm-Liouville:

Now we will assume the return, i.e. let function  be own function of a problem of Storm-Liouville (7)-(9), then whether there will be it own function for a task (6)?

We will find own functions of a regional task (7)-(9). From the equation (7) we have

Believing , we will receive

which common decision has an appearance:

where  - any constants. Having substituted this expression in boundary conditions (8)-(9), we have

,

Therefore,

.

As, that , then ,  i.e. own values of a regional task

are squares of roots of the equation:

,

and own functions have an appearance:

.

Having substituted this expression in the equation (7), we have

.

Having reduced by  both parts of equality, we have

.

We will transform the right part of this equality:

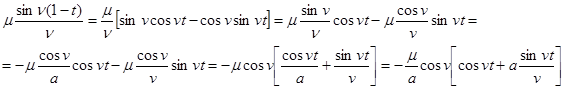
Therefore,

,

from where

,      ,  

   ,   ,

.

Thus, if function  is own function of a problem of Storm Liouville (7)-(9), it is own function of also regional task (6), where

,   .

We proved the following lemma.

Lemma 1 Function  is own function of a regional task (6) in only case when it is own function of a regional problem of Storm-Liouville (7)-(9).

If  the material size, a regional task (6) is self-conjugate therefore the problem of Storm-Liouville also is self-conjugate and therefore has no the attached functions, so rated own functions of a regional task (6) form orthonormalized basis of space .

Lemma 2 If  the material constant, rated own functions of a regional task (6) form orthonormalized basis of space .

We will designate own values of a regional task (5) through , and own functions corresponding to them through  , and own functions of a regional task (4) through , then equality takes place:

Lemma 3 Rated own functions of a regional task:

form orthonormalized basis of space .

Proof. Orthogonality of own functions of a regional task (10)-(11) follows from symmetry of the operator  therefore it is enough to prove completeness of system   of own functions.

Let at some functions  equality take place:

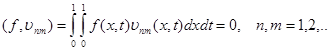
Then owing to Fubini's theorem it is had

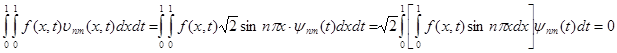
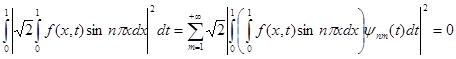
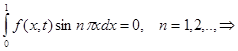
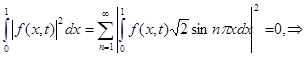
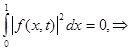
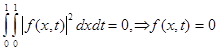
almost everywhere in area , as was to be shown.

In our case  and , therefore we can formulate the following lemma.

Lemma 4 Regional task (5) has an infinite set of own values:

where  - roots of the equations

and corresponding to them own functions

where  - rated coefficients, and .

We will assume that , then  also equality takes place:

,

where . Therefore,

.

Then

i.e. the operator  we will turn. We will find the return operator .

As , that of the last equality follows quite the operator's continuity .

Now we will return to our initial task. The solution of our task has an appearance:

where

 - roots of the equations (12),  - normalizing coefficients.

IV. CONCLUSIONS

As a result of research the following theorem is proved.

Theorem

(a) The mixed task (1)-(3) for the equation of heat conductivity is strongly solvable in space ;

(b) The return operator  is quite continuous on this space and Voltaire;

(c) "Spectral" decomposition takes place:

where

,

 - roots of the equations (12),  - normalizing coefficients,

 - orthonormalized basis of space .

Thus, spectral properties of the indignant operator of heat conductivity are investigated; Fourier submission of solutions of the mixed task for the heat conductivity equation is brought.

Results of article are an essential contribution to development of the general spectral theory of regional tasks for the differential equations.

The received results can be applied in further researches of regional tasks to the differential equations and theories of operators.

2. Elsgolts L.E., 1955, Qualitative methods in the mathematical analysis. GTTI, Moscow, 137-151.

3. Elsgolts L.E., and Norkin S. B., 1971, Introduction to the theory of the differential equations with the deviating argument. Science Publ., Moscow, 116-158.

4. Krasovsky N. N., 1959, Some tasks of the theory of stability of the movement. Fizmatlit Publ., Moscow.

5. Pinni E., 1961, Ordinary differential-difference equations. SILT Publ., Moscow, 88-107.

6. Bellman R., and Cook K.L., 1967, Differential-difference equations. World Publ., Moscow, 271-327.

7. Norkin S. B., 1965, The differential equations of the second order with the late argument. Some questions of the theory of fluctuations of systems with delay. Science Publ., Moscow, 301-318.