Rubber mixing process is extremely complex in its mechanism. In fact, there are two basic processes combined, namely: mixing and dispersing with a simultaneous increase in the specific surface of ​​the contact between the blend components.

The process of mixing the ingredients with rubber compounds is a critical stage of rubber production technology (Amash et al., 2001, Barkanui et al., 2011, Erman et al., 2013). The intensity of the rubber mixing process fixes main indicators of quality of finished rubber, which is used in various fields of human activity - from transport to modern medicine and life.

Physical mechanisms of rubber mixing processes and rubber production are based of the regularities of rheology of viscous flow and deformation of polymers (ter Brinke et al., 2003, Nakajima, 1994, Kaewsakul, 2011, Blackley, 1983). The mixing process occurs in conditions of non-stationary field of deformation speed and temperature. It is accompanied by changes in the internal structure of the polymers and their physical and chemical properties.

It can be assigned two groups of problems linked to the investigation of the mixing process [2, 4].

The first problem is in studying the characteristics of the components to be mixed, i.e., in determining the quality of the mixture, and the second problem is in the description of the process of changing the quality over time (Chukwu, 2011, Nazir, 1989).

There are a lot of approaches to the classification of mechanisms of mixing disperse materials. Mixing processes can be classified by temporary phases of the mixing device. In the early stages of the mixing process the convective mixing dominates, what manifests in the displacement of whole groups and layers of components into the working volume (Rodgers, 2004, White and Kim, 2008).  

The rates of convective mixing and diffusion transfer become comparable only after the initial distribution of the components into the working volume (Youwai  and Bergado , 2003).

The diffusion transfer at this stage is not intensive, as the specific interface between the components is small. Segregation (separation) of the mixture at this time is also negligible due to the immobility of the particles inside the movable layers. The mixing process mainly determines the character of the movement of components in a mixer.

Diffusive mixing becomes prevalent when the interface contact between the phases reaches a certain value. In the case of mixtures of dispersed solids with different physical-mechanical properties, as it occurs generally  in practice, there is a difference in movement trends of different components (Sui et al., 2007), and  in a temp of accumulation of particles of the same type at different areas in  the working volume of a mixer. That is, the segregation begins to affect the course of mixing.

Therefore, to create  a general mathematical model of the process, including a full system of differential equations and boundary conditions, and, especially, to solve such a system, are not possible to date [98].

So the studies related to the development of simplified mathematical models that would clarify the physical basis and reflect the most important observable and measurable characteristics of the process are of particular relevance.

The objectives of this work are to carry out the theoretical description of the mixing which is accompanied by dispersing the polymer blends and to submit on this basis the methods of engineering calculating the apparatuses for mixing the ingredients of rubber mixtures.

II. MATERIAL AND METHODS

The simplest model can be based on a model of dispersive mixing on the approximation of first-order reaction (Rodgers, 2004). Such an approach is acceptable, however, only at the initial stages of mixing and can not estimate the kinetic characteristics of the process.

In this paper we propose an approach to modeling the process of dispersing mixing, based on the concept of generalized Brownian motion of the particles mix ingredients (Feder, 1986, Mandelbrot and Van Ness, 1968). The random walk of particles of ingredients can be described as follows.

At each time interval  with a typical duration determined by the energy consumption for mixing, the probability of a particle drift   is defined using a Gaussian, i.e. normal probability of the distribution (Feder, 1986)

 ,           (1)

Here is  the characteristic diffusion coefficient which  obeys the Einstein formula:

 ,        (2)

where  is the variance of the random variable.

Then the probability of distribution of dispersing mixing is given by:

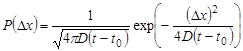 ,          (3)

In dimensionless form the corresponding movement reads

 ,         (4)

The essence of the concept of generalized Brownian motion over fractal manifolds, which are structures with very complex geometry, is that the relation (4) is replaced by the following (Feder, 1986, Mandelbrot and Van Ness, 1968).

 ,        (5)

where is the composite index which is not equal to 0.5 in the general case .

The case  corresponds to an independent increments and describes the usual Brownian motion . The proposed approach, in contrast to the case of simple Brownian motion, allows to consider the prehistory of the mixing process with the help of  varying the index . Hence it is possible to describe correctly the most important feature of a dispersing polymer blend mixing the ingredients, namely the change in its statistical characteristics during the mixing process, and the characteristic time  acquires  sense of the relaxation time.

Then the process of particle drift  on mean statistical approximation obeys

 ,        (6)

Hence the estimate of the standard deviation reads

 ,            (7)

Let us introduce the dimensionless time coordinate  and write the law of generalized Brownian motion in the form (Mandelbrot and Van Ness, 1968, Mandelbrot and Wallis, 1969)

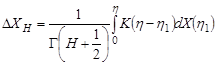 ,          (8)

Here  is the gamma-function.

According to this definion a value of random function at the moment  depends on all preceding moments of the usual normal random process with zerouth average and unitary disparsion.  

The kernel of the nonlocal relation (8), can be defined as follows:

 ,        (9)

Discrete analog of this law for approximate calculations and computer experiment can be obtained by the methods of (Feder, 1986)

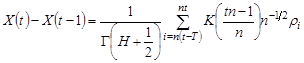 ,          (10)

where - a set of normally distributed random variables .

Thus defined mixing law is nonlocal in the sense that when the parameter the mixing intensity at any given time  depends on the pre-history of the process, i.e. on the kinetic characteristics at all preceding moments.

For  the correlation between past and future deviations is absent. And the phenomena of persistence or non-persistence can be observed for . The persistence which is typical for means the main tendency in system deviations will be maintained.

III. RESULTS

The main hypothesis accepted in this work is that diffusion process under the dispersing mixing can be described with the help of mathematical technique of generalized Brownian diffusion.  

Important feature of the dispersing mixing is the principal dependence of the effective diffusion coefficient (mixing coefficient) on time.  With the proposed model, this feature has been modelled using the coefficient of anomalous fractal diffusion

 ,     (11)

Figure 1 shows some typical graphs of evolution of the effective diffusion coefficient in time.

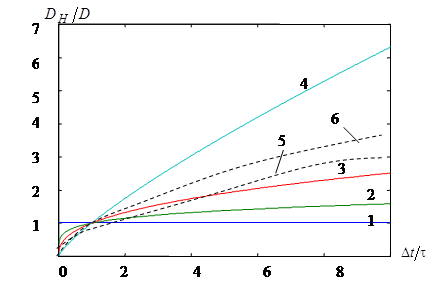
 1- ; 2- ; 3- ; 4-

  Dotted curves depict the experimental data: 5- rubber 1; 6- rubber 2

Figure 1: The effective diffusion coefficient as a function of time for persistence systems

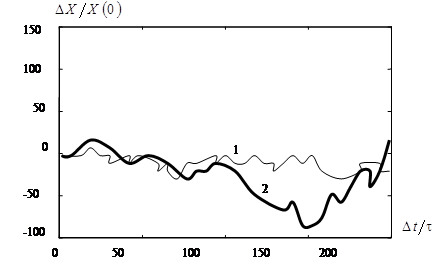
Figure 2: The typical drifts of particles while mixing (1- simple mixing; 2- dispersing mixing)

Since the model predicts an increase in the effective diffusion coefficient in time, respectively, the range of variations of the particles coordinates increases in time too (Figure 2).

IV. CONCLUSIONS

The regularities of the process of dispersing mixing the ingredients with raw rubber are principally different from the process of simple mixing which is not accompanied by dispersing particles system in the blend. The main results and scientific novelty of the work are the following. The stochastic model of dispersive mixing of polymer blends has been carried out. On the basis of approach of the generalized diffusion the expressions for effective diffusion coefficient under dispersive mixing of the ingredients of rubber compounds have been obtained.  The regularities of the diffusion coefficient time evolution have been also studied.  During the experiments the mixing process for blends on the base of two types of rubbers has been investigated. The first one is synthetic methyl-styrene rubber with the methyl-styrene content of 30% (rubber 1), and the second is synthetic divinyl rubber- rubber 2.  The results of experiments confirm that the theory of complex process of dispersing mixing can be built with the help of the model of generalized Brownian diffusion over the fractal media.  The composite index plays a role of the control parameter in this mathematical technique.

2. Barkanui A., Nemeth S., Lakatos B., 2011, Effects of Mixing on the Formation of Polymer Particles in Suspension Polymerization, Chem. Eng. Trans. (CET), vol. 24, 613-619.

3. Blackley D.C., 1983, Synthetic Rubbers: Their Chemistry and Technology, Appl. Sci. Publ. Ltd, London, UK.

4. Brinke J.W., Debnath S.C., Reuvekamp L.A.E.M., Noordermeer J.W.M., 2003, Mechanistic aspects of the role of coupling agents in silica-rubber composites, Composites Science and Technology, vol. 63, 1165-1174.

5. Chukwu M.N., Madufor I.C., Ayo M.D., Ekebafe L.O., 2011, Effect of Stearic Acid Level on the Physical Properties of Natural Rubber Vulkanisate, The Pacific Journal of Science and Technology, vol. 12, No 1, 344-350.

6. Erman B., Mark J.E., Roland C.M., 2013, The Science and Technology of Rubber, Academic Press, Oxford, UK.

7. Feder J., 1986, Fractals, Plenum Press, New York and London.

8. Kaewsakul W., Sahakaro K., Dierkes W.K., Noordermeer J.W.M., 2011, Optimization of mixing conditions for silica-reinforced natural rubber tire tread compounds, Proc. of 180th Technical Meeting of the Rubber Division of the Amer. Chem. Soc., Clevlend, OH, USA.

9. Mandelbrot B.B. and Van Ness J.V., 1968, Fractional Brownian motions, fractional noises and applications, SIAM Rev., vol. 10, 422-437.

10. Mandelbrot B.B. and Wallis J.R., 1969, Computer experiments with fractional Gaussian noises. Part 3, Mathematical appendix, Water. Resour. Res., vol. 5, 260-267.

11. Mandelbrot B.B. and Wallis J.R., 1969, Computer experiments with fractional Gaussian noises. Part 1, Averages and variances, Water. Resour. Res., vol. 5, 228-241.

12. Mandelbrot B.B. and Wallis J.R., 1969, Computer experiments with fractional Gaussian noises. Part 2, Rescaled ranges and spectra, Water. Resour. Res., vol. 5, 242-259.

13. Nakajima N., 1994, The Science and Practice of Rubber Mixing, RAPRA tech. Ltd.

14. Nasir Z.A. and Ratnan C.T., 1989, Epoxidized Natural Rubber Blends, Jour. Appl. Polymer Sci., vol. 38, 1219-1227.

15. Rodgers B., 2004, Rubber Compounding: Chemistry and Applications, Marcel Dekker, Inc. New York.

16. Sui G., Zhong W., Yang X., Zhao S., 2007, Processing and Material Characteristics of a Carbon-Nanotube-Reinforced Natural Rubber, Macromol. Mater. Eng., vol. 292, 1020-1026.

17. White J.L., Kim K.-J., 2008, Thermoplastic and Rubber Compounds Carl HanserVerlag, Munich.

18. Wu Y-P, Ma Y., Wang Y-Q., Zhang L-Q, 2004, Effects of Characteristics of Rubber, Mixing and Vulcanization on the Structure and Properties of Rubber/ Clay Nanocomposites by Melt Blending, Macromol. Mater. Eng., vol. 289, 890-894.

19. Youwai S. and Bergado D.T., 2003, Strength and deformation characteristics of shredded rubber tire-sand mixtures, Can. Geotech. J., vol. 40, 254-264.