1. Statement of the problem. Let and be measurable on - periodic functions. Consider the class of functions , such that

, ;

in a case of we have the classical Lebesgue spaces ; here .

Put

,

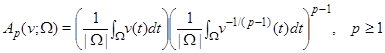where is an arbitrary interval, and the multiplier for is assumed to be , by definition. We say that - condition of Muckenhoupt-Rosenblum ([3], [5]) is fullfiled and use the notation , if , .

In this paper, as in [3], [5], we assume that . Excluding from consideration the trivial case of , we obtain

for (),

since otherwise , whence almost everywhere (a.e.).

Now we can assume that each is also a function of class , since

by the Holder's inequality for and by agreement of

, when .

Let СС the space of - periodic continuous functions. Construct on the spaces (, and С the semigroup of bounded linear operators, commuting with a group of real shifts along the independent variable, which transform or С, respectively, into itself. Consider the Fourier series

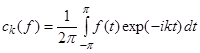, (1)

of any ( or С. According to the general theory of trigonometric semigroups

([2], p.561, Theorem 2.30.1) represents a transform by means of sequence of some multiplicators:

, (2)

and . If, moreover, () is weakly measurable, then is continuous at a strong operator topology. The proof given in [2] for classes C and , remains valid for (,, since it based only on property of commutation of operator with shifts, its linearity and boundedness.

Further, according to the Theorem 4.17.3 ([2], p.159), if is weakly measurable, then has an exponential form. Namely, the Dirichlet representation

(3)

of semigroup is valid. Here be some sequence of complex numbers,

Conversely, a family of operators defined by (3), represents a semigroup of bounded linear operators, commuting with shifts. This semigroup is continuous for at a strong operator topology.

In particular ([1], p 698), a family of convolutions

generates such semigroop; here is a so-called theta-function.

We consider the problem of effective sufficient conditions on multipliers of exponential type, generating the corresponding semigroup of operators. We offer a solution to this problem in a case of a sequences of real numbers {} for operators from to (,, or from C to C. In connection with the problem of convergence domain (3), we show that for almost all values of x on a dedicated multipliers class.

2. Semigroups of operators on , Assume

, , (4)

where and function increases to . Let this growth is so rapid that

, . (5)

Considering the sequence

,, (6)

(see (2)) as a method of summation of Fourier series (1), we note that for (6) it is obviously fulfilled the regularity conditions ([4], p.79)

=1; ; (7)

=0; (8)

and

. (9)

The simplest is the case of , We will be more convenient to apply notation for instead .

Theorem 1. Let the sequence , defined by (4) satisfies the condition (5). If , than a family , where

, , (10)

represents a semigroup of linear operators from to , uniformly bounded (with respect to ), commuting with real shifts, and continuous in the strong operator topology. The continuity is maintained during , namely

. (11)

Proof. We will show the boundedness (10) from to . Let be the sequence of partial sums of the Fourier series (1). Using (4), (6), the integral form of the Fourier coefficients (1) and the Abel transform, we obtain for almost all values of x

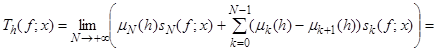
, (12)

since the relation , holds a.e. ([7], p.155), and (5) is fulfilled.

If we use now the estimate ([3], Theorem 8)

; ,

then the uniformly boundedness of operators (10) follows from (12) and condition (9) of regularity of the summation method. Here and later on will represent constants, depending only on clearly indicated indexes.

The continuity in the strong operator topology for all can be proved in the standard way (see the reasoning in the proof of Theorem 2.30.2 , [2], p.563). The assertion of the theorem is valid now for all The relation (11) follows from the convergence

()

([3], Theorem 8) and regularity of the summation method (6).

3. Estimates for the norms of maximal operators.

Theorem 2. Suppose that for the sequence defined by (4), the condition (5) holds, and for all . Then the family (10) represents the semigroup of bounded linear operators from C to C and from to (). This semigroup commutes with real shifts and it is continuous (for ) in the strong operator topology. Furthermore,

(13)

and the estimates

(, ); (14)

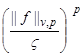(, ) (15)

hold; here

.

The estimate (14) does not valid, generally speaking, for ; in this case

. (16)

Further, the relation

= (17)

holds

а) in the metric of ;

б) in the metric of (,);

в) -almost everywhere for each (,).

Теорема 3. Let the condition (5) is valid,

(18)

and function

(19)

for changes sign a finite number of times. Then the assertions of Theorem 2 hold.

You can specify the nature of the convergence points in (17): in each of the Lebesgue points of function (,); see [6].

Proof of both theorems is based on the estimate ([7], volume 1, p.251)

, (20)

where

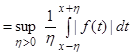
is maximal function of Hardy-Littlewood,

,

and is a sequence of Fejer means of Fourier series

(21)

In particular,

. (22)

Apply again the Abel transform to the right side of (12):

{+

+. (23)

According to (6), (4) and the mean value theorem, we find that the expression is the value of the function in a point , . Applying twice the same theorem, we find that the expression is the value of the function in a point ;

Under the conditions of Theorem 2, we have (see (19)), and therefore the sequence (6) is convex. Then ([7], volume 1, p.155)

, (24)

and we have (as a result of the double application of the Abel transform)

. (25)

Using (24), (25) and (8), (23) we obtain for almost all x the estimate . Then, according to (22) and (20), we have, respectively, (13) and

.

We obtain now the same estimate for under the conditions of Theorem 3. In view of the condition on the function (19), the sequence (6) is a piecewise-convex, and hence convex for sufficiently large values of k. Therefore, the relation (24) remains valid, and (23) takes form

. (26)

Then by (26)

(27)

for almost all x. The sum in right side of (27) will be equal to a finite sum of expressions

where are some positive integers, .

Now, according to (18), the sum in right side of (27) does not exceed some constant. Hence, under the conditions of Theorem 3 we obtain the inequality

(28)

for almost all x. By the results of B.Muckenhoupt [5], the estimates

, (29)

and

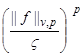, . (30)

hold for . Hence, under the conditions of Theorems 2–3, the estimates (14) and (15) follow from (28), (29), (30). The relation (13) remains valid too by (22).

Assume ; we obtain from (26) by a change of variables :

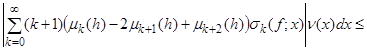
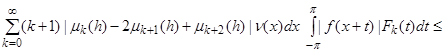
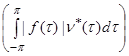
; (31)

here

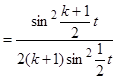
is the integral kernel (Fejer kernel) of means (21) and is the maximal Hardy- Littlewood function for the weight. As is well known ([5]), -condition is equivalent to the relation , which carried out for almost all x. Taking in account the estimates for the sum in the right part of (31), obtained above, we will have

, ,

which proves (16).

According to the theorem of Banach-Steinhaus, the convergence of , in the strong operator topology, i.e. the validity of (17) in the metrics of and (,), follows from the uniformly boundedness of norms of operators (see. (13), (14), (16)) and the relation (7).

The convergence -almost everywhere follows by the standard way (see [7], vol. 2, p.470) from the estimate of weak type (15) and the convergence in the corresponding strong operator topology.

Theorems 2 and 3 are proved.

2.Hille E., Phillips R. Funkcional'nyj analiz i polugruppy (Functional analysis and semigroops). –Moscow: Izdatel'stvo inostrannoj literatury. –1962. – 829 p. (in Russian).

3.Hunt R., Muckenhoupt B. , Wheeden R. Weighted norm inequalities for conjugate function and Hilbert transform //Trans. Amer. Math. Soc. – 1973. – Vol.176. – Р. 227-251.

4. Kuk P. Beskonechnye matricy i prostranstva posledovatel'nostej (Infinite matrices and se¬quence spaces). –Moscow: GIFML. –1960. – 471 p. (in Russian).

5. Muckenhoupt B. Weighted norm inequalities for the Hardy maximal function //Trans. Amer. Math. Soc. –1972. – Vol.165. –P. 207- 226.

6. Osilenker B.P., Nakhman A.D. Behavior of exponential means of the Fourier series and Conjugated Fourier series in Lebesgue points //Vestnik MGSU [Proceedings of Moscow State University of Civil Engineering]. – 2014. –№ 10. – Р. 54 - 63.

7. Zygmund A. Trigonometricheskie ryady (Trigonometric series). –Moscow: “Mir”. –1965. –Vol.1 -615p., vol.2 - 537 p. (in Russian).