About Us
Executive Editor:Publishing house "Academy of Natural History"
Editorial Board:
Asgarov S. (Azerbaijan), Alakbarov M. (Azerbaijan), Aliev Z. (Azerbaijan), Babayev N. (Uzbekistan), Chiladze G. (Georgia), Datskovsky I. (Israel), Garbuz I. (Moldova), Gleizer S. (Germany), Ershina A. (Kazakhstan), Kobzev D. (Switzerland), Kohl O. (Germany), Ktshanyan M. (Armenia), Lande D. (Ukraine), Ledvanov M. (Russia), Makats V. (Ukraine), Miletic L. (Serbia), Moskovkin V. (Ukraine), Murzagaliyeva A. (Kazakhstan), Novikov A. (Ukraine), Rahimov R. (Uzbekistan), Romanchuk A. (Ukraine), Shamshiev B. (Kyrgyzstan), Usheva M. (Bulgaria), Vasileva M. (Bulgar).
Phisics and Mathematics
Tests of machined cylindrical samples of cadmium on fatigue for three values of cyclic loading frequency ω [1-3]. The obtained data presented in figure show an increase in cyclic strength with increasing ω (Fig. 1).

Fig. 1. (a) Fatigue curves and (b, c) microstructure of cadmium at t = 20°C. (a) ω, Hz: (1) 0.033, (2) 1.0, and (3) 46.7; (b, c)(x 600) σ = 36 MPa, N = 103, ω = (b) 0.033 Hz and (c) 46.7 Hz
Apply the interpolation function for the experimental parameter dependencies of the fatigue resistance of the material to the frequency of loading cycles, i.e. tgαw=f(ω). These dependences allow one to determine the value tgαw at any frequency of load cycles within those experimental data are available. In other words, there is no need to conduct the experiment, if the frequency of the loading cycles it is not, but the value of ω is included in the range of values for which experimental data are. The mathematical expression for this purpose looks like this:
tgαw=G0 + G1 (ω−ω0) + G2 (ω−ω0) ( ω−ω1), (1)
continue to expand it:
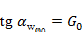 ;
; 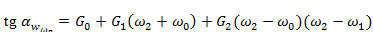 ; (2)
; (2)
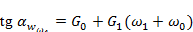 ; (3)
; (3)
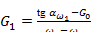 ; (4)
; (4)
Taking the experimental data for cadmium in Fig. 1 and assigning the relevant values ωi and 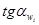 we have:
we have:
ω0=0, 033; ω1=1; ω2=46, 7 Гц;
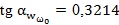 ;
;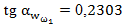 ;
; 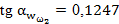
The calculation will get the coefficients of the expression:
G0=0,3214; G1= − 9,4238·10-2; G2=1,9724·10-3.
Substituting the numerical values into the expression (1) we get:
tgαw(ω)|Cd= 0,3246 − 9,6276·10-2 ω + 1,9724·10-3 ω2. (6)
2. Mylnikov V.V., Shetulov D.I., Chernyshov E.A. Variation in faktors of fatigue resistance for som pure metals as a function of the freguensy of loading sycles // Russ. J. Non-Ferr. Met. 2010. Vol. 51. P. 237–242.
3. Mylnikov V.V., Shetulov D.I., Chernyshov E.A. Speed Effect upon Varying the Cyclic Loading Frequency for Certain Pure Metals // Russ. J. Non-Ferr. Met. 2015. Vol. 56. No. 6. P. 627–632.
Mylnikov V.V., Shetulov D.I., Pronin A.I., Kondrashkin O.B., Chernyshov E.A. EXPRESS ESTIMATION OF PARAMETERS OF FATIGUE RESISTANCE. International Journal Of Applied And Fundamental Research. – 2017. – № 3 –
URL: www.science-sd.com/471-25296 (11.02.2026).










 PDF
PDF