Abstract. For the linear means of the Fourier series a family of majorant operators 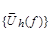is constructed. Their weight-norm estimates are obtained. In the case of exponential means we obtain a relation of the form 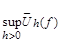~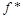, where is the maximal Hardy operator.

Keywords: majorant of means, weighted estimates, maximal function

1. The majorant of the means of Fourier series. We consider an arbitrary 2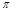-periodic summable on 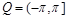function 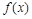, its Fourier coefficients

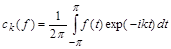
and Fourier series

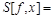
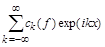. (1.1)

In various problems of analysis, the problem arises of investigating the behavior for families of linear means of the series (1.1)

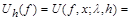
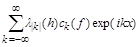, (1.2)

where

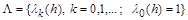(1.3)

is an infinite, generally speaking, arbitrary sequence ("summing sequence"), determined by the values of parameter 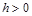. In the case of discrete parameter 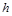, the close problems (namely, the summability of Fourier series at Lebesgue points and uniformly on the continuity interval of function) many authors have studied (see [1] and the bibliography there) .The most important examples of families (1.2) are the Poisson-Abel means, generated by the summing sequence 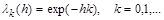([2], pp. 160-165).

Set

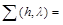
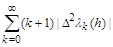and .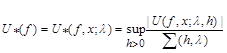

We introduce the Fejer kernel ([2], p.86, 148-149):

.

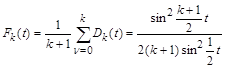Denote

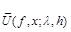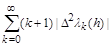
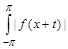
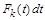=, (1.4)

where 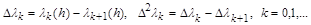are the first and second (respectively) finite differences of the elements of the sequence (1.3); let

.

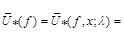
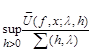Lemma 1.1. If the conditions

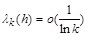(1.5)

and

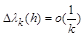
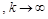, (1.6)

are fulfilled, then the estimate

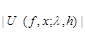
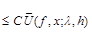
holds at each point x.

The proof follows from the representation

=,

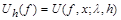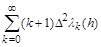
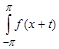
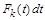obtained on the basis of conditions (1.5), (1.6).

Remark 1.1. The advantage of considering the operator (1.4), which is majorant for (1.2), is that the Fejér means of the Fourier series (the means (1.2) with the integral Fejer kernel) are well studied, and this circumstance facilitates the possibility of transferring some classical results to (1.2).

2. Weighted 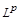-estimations of the majorant. Let (see [3]) 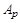be the class of functions 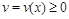that are summable on 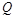and 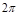-periodic,

, ,

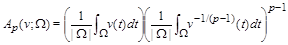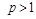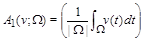
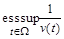and .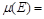

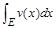Consider the spaces 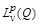with norm

, .

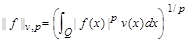
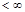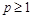Theorem 2.1. Let the conditions (1.5), (1.6) are fulfilled and 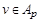. Then the operators 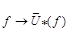are bounded in 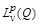, , 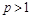and

, .

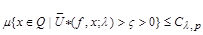
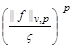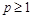Here and in the sequel C are constants (generally speaking, distinct), which can depend only on explicitly indicated indices.

The proof of the theorem follows from the estimate

.

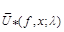
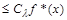where ([2], p. 58-61)

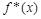
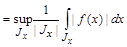
is the maximal Hardy function, and the supremum is taken over all intervals 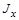with Lebesgue measure 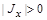, containing an arbitrarily chosen point x.

3. Exponential summation methods. We consider now the semi-continuous summation methods corresponding to the case

, .

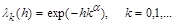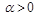Denote

= ;

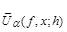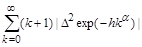
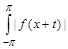
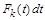let

.

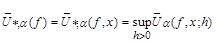Theorem 3.1. For each 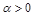there exist positive constants 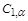and 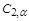, such that

.

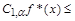
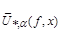
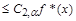Theorem 3.2. For each 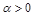and 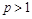the following statements are equivalent:

1) ;

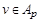2) the estimate

.

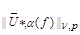
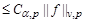holds.

If 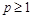, then the following statements are equivalent:

1) ;

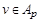2) , .

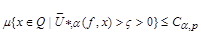
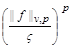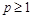The assertions of Theorem 3.2 are the immediate corollaries of Theorem 3.1 and the results of B. Mackenhoupt [3].

2. Zygmund A. Trigonometricheskie ryady (Trigonometric series). –Moscow: “Mir”. –1965. –Vol.1 -615p. (in Russian).

3. Muckenhoupt B. Weighted norm inequalities for the Hardy maximal function //Trans. Amer. Math. Soc. –1972. – Vol.165. –P. 207- 226.