Abstract

The article affirms one of the characteristic fundamental properties of modern research in new directions of their development on the basis of automatic discrete time, which limits the possibility of the appearance of new transitions in elementary memory.

The article discusses the principle of hierarchical program management, which extends the possibilities of simultaneous processing of hierarchical information.

On the basis of the principle of hierarchical program management, multi-level abstract automata working in automatic continuous time and capable of processing and storing hierarchical information in parallel are considered

Keywords: program management principle, program storage principle in machine memory, automatic discrete time, hierarchical program management principle, multi-level abstract automata, automatic continuous time

INTRODUCTION

For the first time the principle of program management was proposed by the British scientist Charles Babbage in the construction of an analytical machine in the 30s of the XIX century. It consisted in the fact that information was divided into two types: processing (data) and control (program).

In 1945, the American scientist J. von Neumann supplemented it with the principle of a program stored in memory, thus completing the theoretical justification for the possibility of creating universal technical means for automating computational work [1].

It is important to note that the calculations made by the computer's processor are determined by the program's commands. It is the program commands that "configure" the computer to obtain the necessary results. Replacement of commands in the program can lead to changes in the functions of the computer. Consequently, the variety of subsets of commands and programs executed in the computer determines a class of functions that are capable of effectively implementing algorithms for a particular class of tasks.

At the present time, the capabilities of computers are growing [2]. They strive to find new capabilities of the element base for integrated circuits based on multifunctional memory circuits and analogs of a biological neuron [3-5]. They try to move away from the Neumann architecture for the purpose of compatibility of operations (pipeline processing of information), parallelization of algorithms (multiprocessor computers), development of interpretation systems (introduction of non-traditional means of addressing and operations over information), etc. [4].

One of the characteristic fundamental properties of these modern studies in new directions of their development is the preservation of automatic discrete time, which limits the possibility of the appearance of new transitions in elementary memory.

One of the proposals for expanding the possibilities for a qualitatively new basis for information processing was the principle of hierarchical program management, proposed by Prof. Marakhovsky LF in 1996 [6].

THE PRINCIPLE OF HIERARCHICAL PROGRAM MANAGEMENT

The principle of hierarchical program management is that the information processed and managed is divided into a local and a general, where the management information is vertically linked from the general information to the local information and processed simultaneously with it (in parallel).

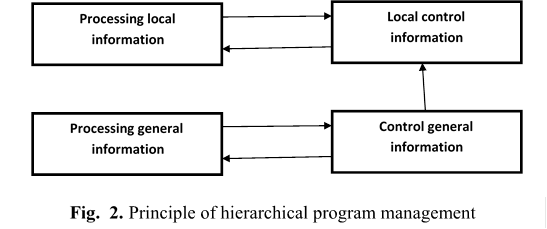
One of the main temporal characteristics of processing hierarchical information in this case is faster processing of local information in relation to the general, and one of the functional characteristics is the change in the algorithm for processing the multifunctional local information, depending on the simultaneous change in the processing of general information.

General information can also be presented as local and general, increasing the number of levels of processing hierarchical information. Such a hierarchical separation of information is finite and possible up to a certain minimum amount of general information.

Local information can be processed unambiguously, probably or unclearly, in the hierarchical program management principle. General ("root") information should be processed unambiguously and determine the mode of processing of local information.

To process the hierarchical memory, we had to abandon the limitations of the automatic discrete time and proceed to automatic continuous time, which allowed us to expand the range of transitions in multi-level automata.

MULTILEVEL ABSTRACT AUTOMATA

Open multifunctional automata of Marakhovsky 1, 2 and 3, having two sets of input alphabets: X - information input alphabet and E - preserving the input alphabet, can be tuned by another open multifunction machine through a set of letters ej(ej E) preserving the input alphabet to function in a certain block (subset) of its states. In this case, a multilevel (hierarchical) structure of the F-automaton from open multifunctional subautomata Si (i = 1, 2, ..., n) is formed. The organization of such a combined structure of the hierarchical automaton (IA) is shown in Fig. 3.

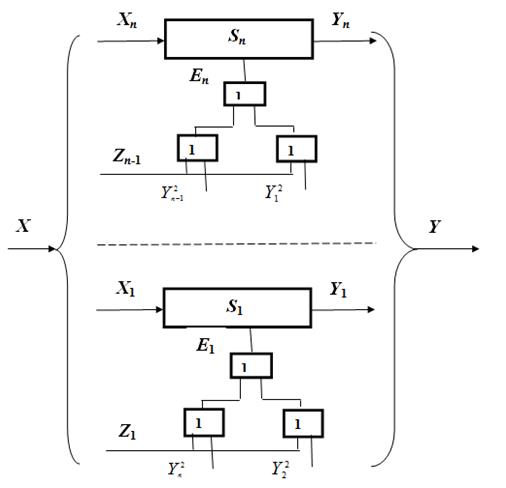
Fig. 3. Hierarchical abstract Fi-automaton

Each multifunctional subautomaton Si (i = 1, 2, ..., n) of a hierarchical abstract F-automaton can pass from one state to another in parallel with other subautomata of IA (Figure 3). The functioning of the Si subautomata in a particular subset of states can be changed by the effects of the input letters of the information alphabet X at the clock time t and the effects of the results of the operation of other subautomata Si IA by the letters of the preserving input alphabet E at the moments of the internal cycle Δ of the automatic continuous time T.

Let us define a multi-level (hierarchical) abstract F-automaton.

Definition. The mathematical model of a hierarchical discrete device with a multifunctional system of memory organization is an abstract hierarchical F-auto-maton, defined as an N-component vector

F= (S1, S2, …, SN), (1)

whose Si components are given by the sixteenth component vector

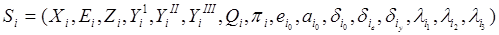(2)

which one

• Xi - a set of information input signals;

• Ei - the set of input signals that save;

• Zi - the set of resolving input signals;

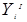• - a set of output signals of type 1;

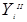• - a set of output signals of type 2;

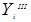• - a set of output signals of type 3;

• Qi is an arbitrary set of states;

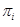• - the set of blocks of states of the subautomata ;

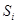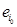• - initial storing the input signal;

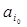• – is the initial state of the Si subautomaton;

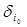• : Qi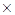 Xi→ Qi is a single-valued transition function;

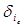• : Qi 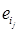→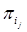- state blocks saving function;

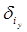• : Qi Ei →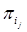- the function of the enlarged transition;

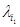• : Qi Xi→ 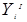- function of outputs type 1;

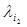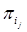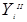• : → – - function of outputs type 2;

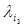• : Qi Ei →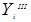– - output function type 3

and defined functionally, as well as the components of the Si structure, by a sixteenth component vector

FA = (X, E, Z, 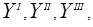Q, 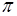, E0, Q0 , F1, F2, F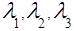3, ) (3)

which one

• X={X1, X2, …, XN} – the set of information input signals;

• E ={E1, E2, …, EN}– is the set of input signals that conserve;

• Zi ={Z1, Z2, …, ZN}– the set of resolving input signals;

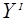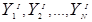• ={}– set of output signals of type 1;

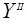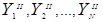• ={}– set of output signals of type 2;

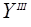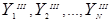• ={}– set of output signals of type 3;

• Q ={ Q1, Q2, …, QN}– is an arbitrary set of states;

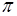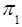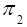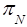• ={,,…, }– the set of blocks of states of the subautomata Si;

• E0=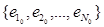 – initial saving the input signal;

• a0 =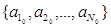 – the initial state of the Si subautomaton;

• F1: Q X→ Q – is a single-valued transition function realizing the mapping DF1 Q X to Q;

• F2: Q еj → πj – is the conservation function of the state blocks, realizing the map DF2 Q еj to πj;

• F3: Q E→ πj – is the coarse transition function realizing the mapping DF3 Q E to πj;

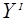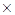• λ1: Q X→ – is a function of outputs of type 1 that implements the mapping Dλ1 Q X on ;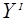

• λ2: πj →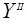– is a function of outputs of type 2, realizing the map Dλ2 πj on ;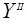

• λ3: Q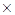 E →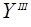– is a function of outputs of type 3 that implements the mapping Dλ3 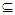Q Е on .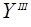

Subautomata Si, realizing their automaton memory on open-type registers, function in automatic continuous time T.

At the initial clock moment t0, all the Si subautomata are set to the initial state a0 by the corresponding input signal 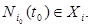During the subsequent internal clock cycle Δ0, the initial state a0 is preserved under the influence of the initial input 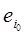(?0) input signals. The union of the states ai of the Si subautomata determines the states ai of the hierarchical automaton at a given clock time ti or Δi of the automatic continuous time Ti.

In the hierarchical automaton A, at the time ti, all or only some Si subautomata can perform single-pass functions 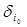, realizing the common function of single-valued transitions F1 of the hierarchical automaton A to the new state 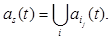During the internal cycle Δi, the Si subautomata can perform the coarse transitions 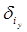,realizing the common transition function F3 of the hierarchical automaton A to a new state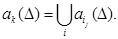

If the Si subautomata do not perform transitions to a new state during the entire outer cycle T, then, consequently, they realize the state conservation function 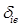, realizing in IA A the joint function of conservation of states F2.

Each of the Si subautomata operates in a certain state block 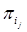of the whole set of its states Qi. The blocks 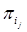of states of Si subautomata form a definite block 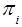of the set of state blocks 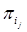in IA A, in which the IA A is functioning at a given time.

A characteristic feature of IA is the possibility of interaction of Si subautomata not only during the clock ti, but also during the internal cycle Δi of the automatic continuous time Ti. The memory of the Si subautomata is a matrix structure in which, during the time ti, under the influence of the information signals хі(t) of the input signals, the Si sub-automaton is able to go from one state to another in one state block 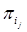(the matrix structure line of the automatic memory circuit). And during the internal cycle Δi, under the influence of the input signals retaining еj(?), the Si sub-automaton is able to go from one state to another in one block μi (the column of the matrix structure of the automatic memory circuit), that is, from a certain state of one block 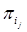to a certain state of another block 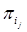states.

Thus, the mathematical model of a multilevel hierarchical automaton A is able to describe the functioning of not only parallel Si, but also their inter-layer interaction by using the letters of the input preserving E alphabet of the Si subautomata.

CONCLUSION

The article discusses the principle of hierarchical program management, which allows you to present multi-level control information with a vertical relationship between levels and the ability to process this information simultaneously.

Management of multi-level abstract automata is described on the basis of the principle of hierarchical program control.

2. Татур В.Ю., 15 лет проекту «СКИФ»: история и итоги // «Академия Тринитаризма», М., Эл № 77-6567, публ.18063, 09.06.2013

3. A. S. Cassidy, P. Merolla, J. V. Arthur, S. Esser, B. Jackson, R. Alvarez-Icaza, P. Datta, J. Sawada, T. M. Wong, V. Feldman, A. Amir, D. Rubin, F. Akopyan, E. McQuinn, W. Risk, and D. S. Modha, “Cognitive computing building block: A versatile and efficient digital neuron model for neurosynaptic cores,” in International Joint Conference on Neural Networks (IJCNN). IEEE, 2013.

4. Мараховский Л. Ф. Основы новой информационной технологии. Фундаментальные основы проектирования реконфигурируемых устройств компьютерных систем и искусственного нейрона: монография. Л. Ф. Мараховский, Н. Л. Михно – Germany: Saarbrcken, LAP LAMBERT, 2012. – 347 с.

5. Marachovsky L.F. Basic Concepts to Build the Next Generation of Reconfigurable Computing Systems – International Journal Of Applied And Fundamental Research. – 2013. – № 2 – URL: www.science-sd.com/455-24170 (20.11.2013). – 6 c.

6. Мараховский Л.Ф. Основы теории проектирования дискретных устройств. Логическое проектирование дискретных устройств на схемах автоматной памяти: монография. – Киев: КГЄУ, 1996.–128 c.