Abstract

In work [1] the mathematical model that describe population of bacteria causing community-acquired pneumonia under the action of antibiotics is offered. In the present work, is presented a visualized computer realization of this model that allows investigate the influence of parameters of bacteria and antibiotic on the bacteria's population size.

Keywords: mathematical model, program realization, visualization, bacteria, antibiotic, health.

1 Introduction

The sensitivity decrease to the action of antibiotics is one of the actual problem of the present medicine. At present, this problem becomes more important as result of uncontrolled use of antibiotics [2].

In the process of adaptation, bacteria acquire a resistance to action of antibiotic. Therefore, further use of the antibiotic is ineffective, because the bacteria continue to multiply and the population increases. It is necessary correctly to calculate concentration of antibiotic for the treatment to avoid disease progression.

This mathematical model shows the ineffective of an antibiotic, provided that the bacteria acquire a resistance to its action, and offers methods of solving this problem.

2 Mathematical model

The bacteria population is divided into two categories: bacteria sensitive to antibiotic action (x1) and bacteria insensitive to antibiotic action (resistant – x2). The antibiotic has bactericidal and bacteriostatic effects. Bacteria multiply with a population increase coefficient a1 и a2 for sensitive and resistant bacteria, respectively. To limit the increase of bacteria population, the life-space limitation coefficients b1 and b2 are introduced. In addition, bacteria mutate from sensitive ones to resistant with coefficient М21 and from resistant ones to sensitive with coefficient М21. Coefficients of antibiotic are efficacy (Oc and Os) and concentration (cc and cs) for bactericidal and bacteriostatic antibiotic respectively.

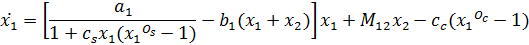
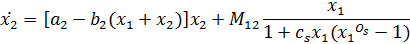
A mathematical model can be described by differential equations and the initial conditions [1]:

  (1)

Description of symbols is presented in the table 1.

Table 1. Coefficient and values of model

3 Program realization of the mathematical model

Systems of equations (1) have been numerically resolved. Below is the main program window, where mathematical model is build and presented (Figure 1). Visualization of mathematical model allow investigating dynamic of population bacteria by changing parameters in given range.

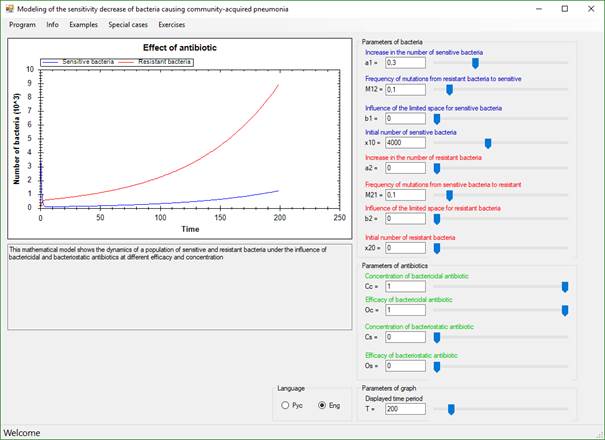
Figure 1. Program for visualization of mathematical model

The main problem of the treatment by antibiotic is the acquisition of resistance property. If bacteria were not adapt, treatment would be successful even with small doses of antibiotic (Figure 2). However, in reality, sensitive bacteria can mutate to resistant ones. As result of this mutation, population of bacteria does not perish even with high dose of antibiotic (Figure 3). If, in this case, surviving bacteria will produce offspring, then the population of bacteria will grow (Figure 4).

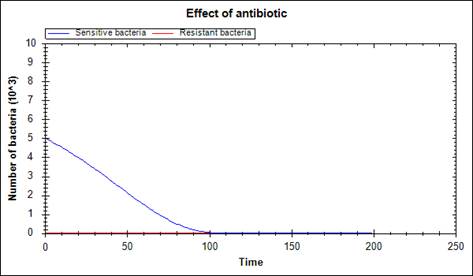
Figure 2. Successful treatment

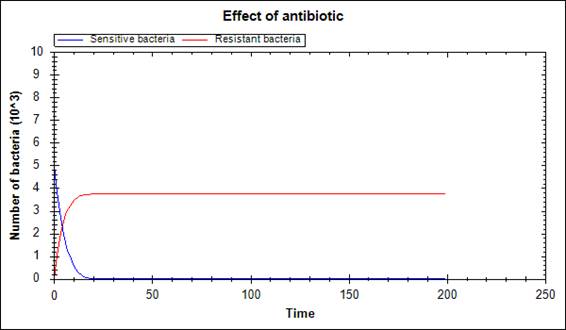
Figure 3. Population of bacteria does not perish.

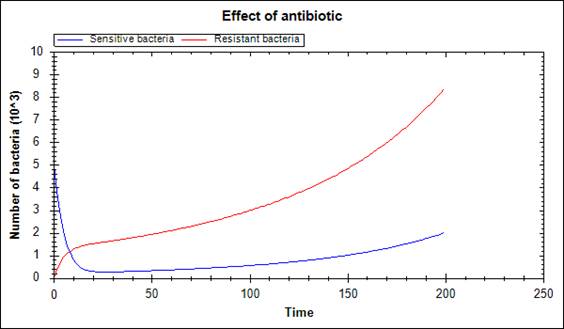
Figure 4. Population of bacteria grows

However, in real situation, living space for bacteria is limited, which allows the antibiotic to destroy the bacteria population (Figure 5).

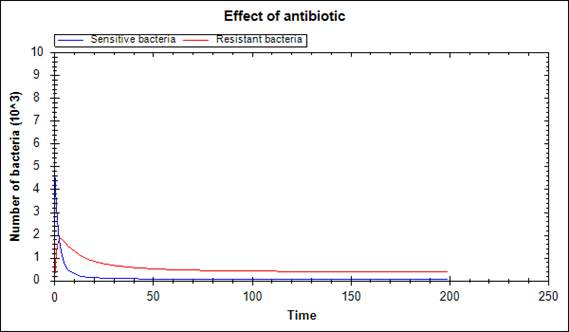
Figure 5. Population of bacteria perish

With a limited living space, with no mutations and antibiotics, this model is equivalent the Lotka-Volterra model of interspecific competition. In this case, the type of bacteria, which has a higher coefficient of population increase, will have a large population (Figure 6). When an antibiotic is introduced, the situation changed on opposite. The resistant bacteria begin to dominate, and the population of sensitive ones decreases (Figure 7).

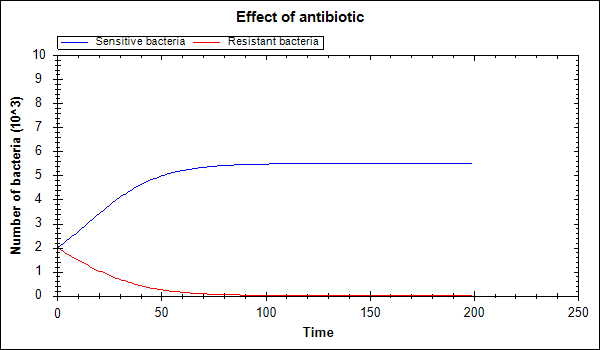
Figure 6. Interspecific competition of bacteria

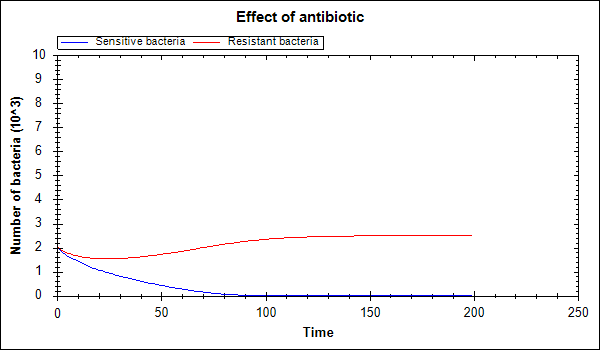
Figure 7. Interspecific competition of bacteria when antibiotic was entered

This happens in real situation when an antibiotic is entered. The number of resistant bacteria begins to grow. To reduce the number of resistant bacteria, it is necessary to stop using the antibiotic. After a while, the system returns to its original situation (Figure 6) and the treatment may be repeated. In addition, an alternative way is to change the antibiotic.

Conclusion

Visualization of the mathematical model describing the acquisition of resistance properties by bacteria demonstrates the reasons for the inefficiency of the antibiotic, which applies in a long period. This model can be used for educational and practical purposes, for example, to find the minimum necessary concentration of antibiotic for providing quality treatment.

2. Goossens H., Ferech M., Vander Stichele R., Elseviers M. Outpatient Antibiotic Use in Europe and Association with Resistance: A Cross-National Database Study. The Lancet, 2005, Vol 365, 579–587. doi:10.1016/S0140 6736(05)17907-0

3. Pechère J.C. Patients’ Interviews and Misuse of Antibiotics. Clinical Infectious Diseases, 2001, 33(Suppl 3), 170–173. doi:10.1086/321844