Abstract. A one-parameter class of generalized Lebesgue points is considered. The means of Fourier series, which are generated by linear semi-continuous summation methods, are introduced. In the case of quasi-convex summing sequences, the convergence of means at each generalized Lebesgue point is established. Estimates of deviations of means from their generating function are proposed.

Keywords: quasi-convex summation methods, deviation estimates, summability almost everywhere

1. Points of summability. Let 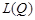be the class of arbitrary 2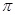-periodic functions 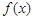, which are summable on ,

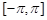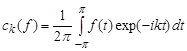
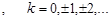
are Fourier coefficients of any such function and

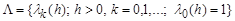(1)

is an infinite, generally speaking, arbitrary sequence determined by the parameter 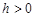values. We study the behavior at 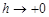of the families of linear means of the Fourier series

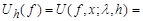
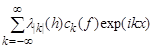(2)

at the points at which

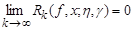. (3)

Here

,

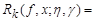
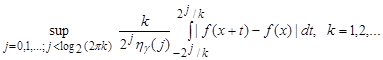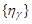is a family of positive functions 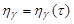, determined by the values of parameter 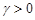and increasing in the arguments 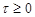and 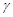; at the same time we assume that 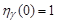and the series

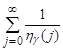(4)

is convergent.

Lemma. The relation (3) holds almost everywhere in 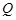for any .

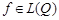The assertion of the lemma (and its analogue for functions of two variables) in the case of 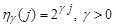, was established in [1]. The points with property (3) are called as generalized Lebesgue points.

2. Estimates of dodge. We will consider the quasi-convex sequences (1), that is, those for which the sum

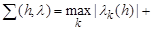
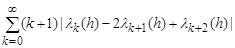
uniformly on h is bounded. In particular, convex (concave) and piecewise convex sequences possess the property of quasi-convexity.

Theorem 1. Let the family of functions, 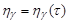, , 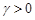be such that the series (4) and

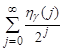
(5)

are convergent. Let also the sequence (1) be quasi-convex and

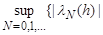
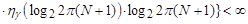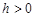(). (6)

Then the series (2) is convergent for all 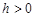at each generalized Lebesgue point, and the estimate

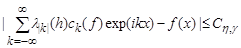
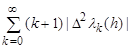
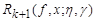
holds.

Here and hereinafter, C denotes constants, generally speaking, different and depending only on explicitly indicated indices.

As examples of functions 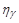satisfying the convergence conditions for series (4), (5), we indicate the following:

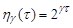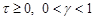,; (7)

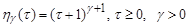. (8)

3. Summability almost everywhere.

Theorem 2. Let the conditions of Theorem 1 are valid and

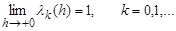
Then the relation

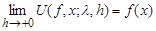
holds at every generalized Lebesgue point, that is, almost everywhere in .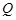

4. Exponential summation methods. Examples. Let now 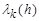=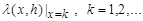, where 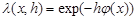, , 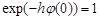and the function 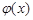is continuous on [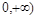and twice differentiable on (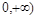. Refer to the examples.

1) Consider 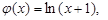then 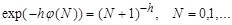, and the summing sequence (1) is convex. If 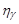defined by the relation (7), then it easy to see what the results of [1] are not applicable to this summation method. The condition (6) is satisfied, however, in the case of (8) with an arbitrary fixed one 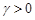. Note, that along with the fact of summability of Fourier series almost everywhere by the method

,

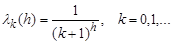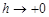
(see [2]) , now the character of summability points is also established.

2) In the case of 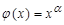, the sequence (1) is convex with 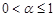and piecewise convex with 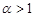; therefore, its quasi-convexity condition is satisfied. Here the relation (6) holds when (7) occurs. Really,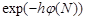 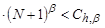, 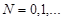with any fixed 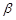, chosen from the condition 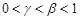. Note that a particular case of the summation method 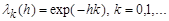is the classical Poisson-Abel method.

2. Nakhman A.D., Osilenker B.P. Exponential methods of summation of Fourier series // Bulletin of TSTU. - 2014. - Vol. 20.- No.1. - P. 101-109.