In recent years, actively developing all kinds of information technologies that are used in education. In this article we consider an example of the use of computer technology in the study of "Conformal mapping" in the course of “Complex Analysis” for the bachelors of the speciality 02.03.01 — mathematics and computer science.

Due to time constraints, in practical preparation classes it is not possible to fully consider the various problems associated with the construction of conformal maps. MAPLE system allows you to overcome the difficulties arising in the study of this topic. In addition to visual solutions, it encourages students to search for new information, as well as independent study of theoretical issues.

Students are invited to solve a number of problems using MAPLE.

The plot package contains a function for conformal mappings: conformal (F, r1, r2, options), where F is a complex procedure or expression; r1, r2 are ranges of the form a..b or name=a..b.

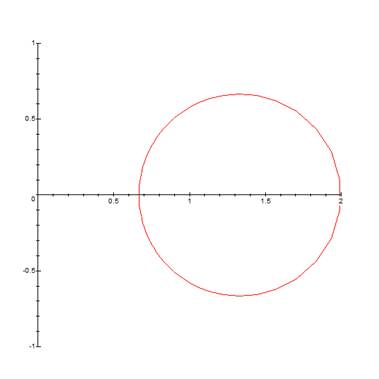
Consider the example of the use of conformal procedure: find image of the circle |z-1|=1/2 by the function w=1/z.

> with(plots): conformal(1/(z+1), z=1/2-I*0..1/2+2*Pi*I, coords=polar, numxy=[64,64], view=[0..2, -1..One]);

Moscow: Editorial URSS. — 2001. — 352 p. [In Russian]

2. Lavrentiev M. A., Shabat B. V. Methods of the theory of functions of a complex variable. — Moscow: Nauka, 1987. — 749 p. [In Russian]

3. Markushevich A. I. Theory of functions of a complex variable. Vol.1. - Englewood Cliffs (N. J.): Prentice-Hall. — 1965. — 474 p.

4. Ivanov V. I., Popov I. Yu. Conformal mappings and their applications. — Moscow :Editorial URSS. –2002— 324 p. [In Russian]