There is a problem of constructing models of the kinetics of phase transitions in two-phase gas-crystal or liquid-crystal systems, and it is desirable that they are free from uncontrolled use of macroscopic characteristics in them that are not applicable to nanostructures. The process of film formation as a result of gas or liquid epitaxy on a crystal substrate, which we simulate by the pseudopotential of the crystal field with the symmetry of the crystal of the substrate, is considered. A set of particles of an unordered phase is considered as a dynamic system of particles in a state of thermodynamic equilibrium with a crystal substrate. At temperatures below critical, a part of the system particles are deposited on a substrate in a state with zero translational momentum. As a result of the interaction of adatoms, nuclei of a new phase are formed on the crystalline surface.

To study the process of deposition of a substance on a substrate, we use the Hamiltonian of the Bose-particle system in the representation of the second quantization 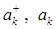and pseudopotential of the form of the substrate field. The no conservation of the number density of particles 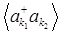in an unordered system is due to the presence of a substrate field, which leads to the appearance of nonzero anomalous means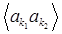, which, at k = 0, determine the concentration of precipitated particles.

To determine the concentration of condensate, we use the method of quasi-averages and two-time Green functions. Solving together the system of equations for the normal and anomalous one-particle Green functions in the mean field approximation, we find ε – the energy of single-particle excitations, and Δ – the gaps in the excitation spectrum of the monolayer of crystalline condensate on the substrate. The appearance of Δ 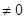is a criterion for the onset of condensation of a disordered phase on a substrate. Solving together the system of equations for the Green's functions, we find the equation for determining the gap 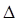in the excitation spectrum of the precipitated crystal lattice.

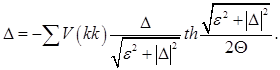(1)

Using equation (1), spinodal of the appearance of thin films on a crystalline surface can be obtained. The energy of single-particle excitations ε is determined by the kinetic energy of the particles and the potential of the substrate field U. The numerical solution of equation (1) was carried out using the Mathcad package. Determining the conditions for the appearance of a nonzero solution of equation (1), spinodals of the appearance of thin films on the substrate surface are obtained for various values of the pair interaction parameters, different substrate potentials U, and also for different substrate temperature.

For the probability density of the distribution of adatoms over levels 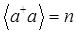from the system of Heisenberg equations of motion for the order parameter of the problem – the shear component of the structural transformation and average level populations; after averaging, we can obtain a nonlinear equation

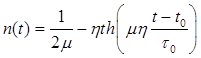, (2)

here τ is the growth delay of the film. This equation is known in the “super radiation” theory as the Rehler–Eberle equation, which at short times has a solution in the form of a kin-like inhomogeneous distribution of adatoms at the boundary of a flat film. Equation (2) was obtained as a solution of the system of equations for the order parameter and conjugate field in the case of a first-order structural phase transition “no structured phase — crystalline film» on the substrate [1]. Expression (2) describes the process of formation of an inhomogeneous kink-like distribution of atoms, which represent the domain wall of the edge of a thin growing film.