The article is a further development of the ideas first established by academicians L.V. Kantorovich [9,10], V.M. Glushkov and developed in future professors V.V. Ivanov, Yu. P. Yatsenko [7,8,11, 13-17], S.K. Girlin [5,12]. There are two basic classes of developing systems (DS) (or evolutionary systems): 1) DS that are already have been created and have initial prehistory, 2) DS that are not have been created and have not initial prehistory. The second class is named originating DS [2]. Each of these classes divides, in turn, on three classes: Artificial DS (ADS) that are have been created by human beings and are functioning with their participation; Natural DS (NDS), in particular, the cell and cell associated objects [14]; and Joined DS (JDS): ADS and NDS as a whole [12]. So we have 6 classes of DS in all. Some examples of ADS are: industry, science, any educational center, including school, college, university, and  education as a whole, art, health services, etc. The examples of NDS are the cell and cell associated objects, a separate plant, a separate organism, a population of animals, the biosphere, etc. We can consider the neosphere (in the sense by academician  V.I. Vernadsky) as JDS that is the combination of two DS, one of which is human activity as ADS and another of which is the other part of our planet as NDS [13, p. 10]. The main elements of ADS are work places (WP). A work place is usually localized in the time and space aggregate of labor functions of the respective ware: material, energy, and information, which should be fulfilled by a respective specialist. The result of WP functioning in industry are various goods and services or products. The main characteristics  or indices of the WP functioning are efficiency (the quantities of products produced per unit expenditure and per unit time). There are three important classes of WP: one that enters the DS from external environment or from other DS, the second reproduces or creates new more effective WP for the DS itself, and the third reproduces external goods with respect to DS. There are two branches of industry: one is called a subsystem A of DS in which DS creates new WP, and the second is called a subsystem B of DS in which DS creates or produces goods and services that are external with respect to DS. The distribution of WP by some control function y(t) between the subsystems A and B is very important. The problem of this optimal distribution was formulated  by V.M. Glushkov.  This problem was investigated in [7]. The main result is for small-term period of the time  the desired y(t) is minimally possible, but for large-term period of the time  the desired y(t) may differ from the minimally possible on the larger initial part of the time segment.

The consideration of distribution between subsystems A and B not only internal, but  external resources too, allowed to generalize mathematical model of  DS [2-6] (in particular, to investigate originating developing systems without given prehistory of DS [2,3]).

A set of the obtained results suggests that it has been created a new science - mathematical theory of development [14].     

We will consider the simplest case of cooperative interaction of  two-product  developing systems. It is the case of passive  systems interaction, at which the systems distribute between itself external resources and not exchanged between itself the products of its functioning. Equations and inequalities of the passively interactive DS look like:

                          (1)

,                      (2)

where i is the number of DS, i=1,2; f(t) is the rate of the resource inflow from the outside at the instant  ; is the rate of arrive of the first new generalized product (internal resource) quantity at the instant  , which provides the fulfillment of the internal functions of DS, that is, restoration of itself and creation of the second kind product (is measured in the units of ;  is a share of  for fulfillment of internal functions in the subsystem A of restoration and perfection of the system as a whole, ; is the efficiency index for functioning of the subsystem A along the channel i.e. the number of units of  created in the unit of time starting from the instant  per one unit of ; is a special temporal bound: the new product creating before  is never used at the instant , but created after  is used entirely;  is the rate of creation of the second kind new generalized product quantity at the instant  , which provides the realization of the external functions of DS;  is coefficient of measure accordance among  f, m, and c; and are similar to and  respectively but for the subsystem B of creation of the second kind product; is the total quantity of the obsolete product at the instant  ; is the starting point for modeling; it is the prehistory on  of DS, for which all the functions are given (their values will be noted by the same symbols but with the sign “0”, e.g. ,

Let

Let us put

_{The equations (1), (2) can be rewritten as}

                                           (3)

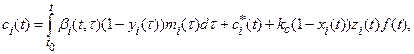                                    (4)

_where

,  

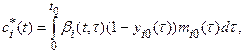
Let

Let us put

 Theorem 1. Let non-negative piecewise continuous functions ,  be given

on  (i.e., the initial prehistory be given), also continuous functions  on ,  positive function  , piecewise nonnegative continuous functions  be given. Then the system (3),(4) has the unique piecewise continuous solution

                  (5)

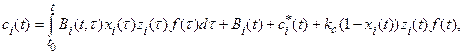
                  (6)

where    

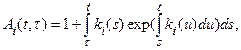
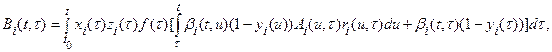
and on  the functions  andare piecewise continuous ,.

Proof. It is similar to the proof [12].

If we put, we can consider the following task: to determine the control  function z*(t) with the restrictions (3), (4), for which the functional

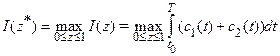
Theorem 2.Under conditions of theorem 1, the functional  I(z)  has the form:

                                                                    (7)

,

, ,

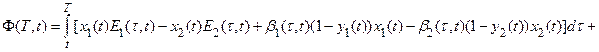
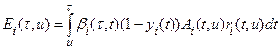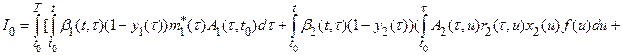
           The required type of functional can be found by the direct substitution of the solution (6).

Theorem 3.If the conditions of theorem 1 are fulfilled, then

The proof of this and the following theorems follow directly from the functional (7)-type.

Theorem 4. If the systems above are identical, any allocation of the external resources between the systems is optimal.

The proof is obvious, because in this case , , and the functional    does not depend on _.

Theorem 5. If  is sufficiently small, the  function  is continuous on the interval , then for maximization of the functional I(z), it is necessary to send all external resources to the system i, i = 1,2, for which  x_i(T) is less, i.e., to the system, in which relative part of external resources, sent to the subsystem of self-perfectionist less (thus, the relative part of external resources, sent to the subsystem B_i of implementation of external function, accordingly is greater).

Corollary. If the function  is continuous on some (T−e,T], e>0, then at the end of any cutting-off of time of planning for maximization of the considered functional, it is necessary to send all external resources to the system, for which relative part of the external _{resources (sent  to the subsystem Bi) is greater.}

Condition A. Let  the functionbe differentiable by variable t on the

_{segment [t0,T] and constants L1 and L2, L1³L2>0, be known and such, that}  .

It is obvious, that for any

Theorem  6. If the condition A is fulfilled and  then on interval  the maximum of the functional I(z) is achieved at z(t) = 1, on interval at z(t) = 0, and on the segment  at.

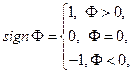
The proof easily follows from the obvious fact, that a maximum of functional  is achieved at , where  and

Let us show that condition A fulfilled, if, for example, the next condition B is fulfilled.

Condition B. Let

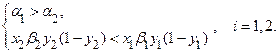
Under condition B

and function  is continuous if Consequently, by the theorem of Weierstrass function  on    has the most negative value (which can be designated through  ) and the least negative value (which can be designated through −).

Condition C. Let  and

Theorem 7. If the condition C is fulfilled and , then the maximum of the functional   is achieved at  on   and at  on   .

As 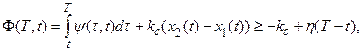 then the proof easily follows from the estimation of sign of function

Remark.The optimization task of the best distributing of external resource examined here between two co-operatively interactive two-product developing systems was decided for the special case:, in  [1].

Conclusion.The got results (theorems 4-7) for the case of passive co-operative two-product DS interaction  are analogical the next first two laws of optimal development of one system [4,14] (we suppose that it is possible to prove statements analogical and to the third law of optimal development).

These laws can be set forth as follows.

First law of optimal development (“law of altruism”). If the size of planning time is small enough, the sought optimum of functional is arrived at the maximally possible (by virtue of limitations of task) use in the subsystem B of internal and external resources for implementation of basic function of the system.

Second law of optimal development (“law of reasonable egoism”  [4,11]). If the size of planning time is great enough, the sought optimum of functional is arrived at the substantial stakes of internal and external resources, using the subsystem of self-perfection on the internal necessities of the system on greater initial part of cutting-off of planning time and maximally possible use in the subsystem B of internal and external resources for implementation of basic function of the system at the end of it. This law was shown out of the theorems at general enough suppositions [5].

Third law of optimal development (“law of hierarchy of priorities”) [13,14]. If the size of planning time is great enough, the sought optimum of functional is arrived at the following priorities of allocation of internal and external resources between the subsystems of developing system: first of all at the larger initial size of planning time the subsystem  (“science”) has priority ( is the subsystem , in which new technologies of system products creation functions of  and  kinds), then at the long time size has priority the subsystem of self-development  (the subsystem, in which new products of the first kind are produced, providing the fulfillment of the internal function of the system – its existence and development itself), and at the end of the planning time  the subsystem B has priority, in which products of the second kind are produced, providing the fulfillment of the main system function to the system).

We`d like to notice that the law of "reasonable egoism" of the system can be considered as clarification of basic principle of communism: "to each - on necessities, from each - to abilities".

2. Гирлин С.К. Моделирование возникающих развивающихся систем // Докл. АН УССР. Сер. А. – 1987. - № 10. – С. 65-67.

3. Гирлин С.К. Лекции по интегральным уравнениям. – Ялта: РИО КГУ. – 168 с.

4. Гирлин С.К., Билюнас А.В. Модель и законы оптимального развития систем // Успехи современного естествознания. – 2011. - № 7. – С. 254-259.

5. Гирлин С.К., Иванов В.В. Моделирование взаимодействия развивающихся систем // Докл. АН УССР. Сер. А. - 1986. - №1. - С. 58-60.

6. Гирлин С.К., Щербина К.П. Моделирование оптимального взаимодействия континуальных развивающихся систем // Успехи современного естествознания. – 2012. - № 4. – С. 32-37.

7. Глушков В.М. , Иванов В.В. Моделирование оптимизации распределения рабочих мест между отраслями производства А и Б. – Кибернетика, 1977, № 6, С. 117-131.

8. Глушков В.М., Иванов В.В., Яненко В.М. Моделирование развивающихся систем. – М.: Наука, 1983. – 350 с

9. Канторович Л.В., Горьков Л.И. О некоторых функциональных уравнениях, возникающих при анализе однопродуктовой экономической модели // Докл. АН СССР. -1959. - 129, № 4. - С. 732-736.

10. Канторович Л.В., Жиянов В.И. Однопродуктовая динамическая модель экономики, учитывающая изменение структуры фондов при наличии технического прогресса // Там же. – 1973. – 211.\, № 6. – С. 1280-1283.

11. Яценко Ю.П. Интегральные модели систем с управляемой памятью.– К.:Наук.думка, 1991. – 220 с.

12. Girlin S.K., Bilunas A.V. Analytic solution for the optimal distribution of external resources between the subsystems of a developing two-product system / Cybernetics and System Analysis, Vol. 48, Issue 6, 2012. – pp. 906-911.

13. Ivanov V.V. Model Development and Optimization. – Dordrecht / Boston / London : Kluwer Academic Publishers, 1999. – 249 pp.

14. Ivanov V.V., Girlin S.K., Korzhova V.N., Yanenko V.M. Further Development of Academician V.M. Glushkov Models and Its Applications // Мат-лы международной научной конференции “Вопросы оптимизации вичислений (ВОВ-XL)”, Кацивели, АР Крым, Украина, 30 сентября – 4 октября, 2013, С. 105-106.

15. Ivanov V.V., Ivanova N.V. Mathematical Models of the Cell and Cell Associated Objects. – Amsterdam: Elsevier, 2006. – 333 pp.

16. Korzhova V.N., Saleh M.F., Ivanov V.V. Mathematical models of information systems developing // Proceedings of The 2nd International Multi-Conference on Complexity, Informatics and Cybernetics, March 27-30, 2011, Orlando Florida, USA. - Vol. 1, pp. 223-228.

17. Yatsenko Yu. Modeling and Optimization of the Lifetime of Technologies / Kluwer Academic Publishers, 1996. – 250 pp.