=                                                 (1)

of  Fourier series s[f]  of  functions f ∈ L. In the definition (1)

,  

are complex  Fourier coefficients of function   f.

We study the problem of  behavior (1) at , when the point is within the boundaries of the angular  domain

The case of  “radial” convergence  at  was investigated in [1].

2. The main result.  Define

;

let  and

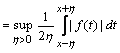
be  Hardy maximal function ([2], vol.1, p.55). 

Theorem 1.  Let the sequence  decreases so rapidly that

                                                  ,                                          (2)

and there is a constant  such that

                                                                                                              (3)

Then for every x the estimate

holds.

       Here and throughout the paper  will represent  constants, which depend only on the explicitly specified indexes.      

3. -estimates.  Let

be a norm in  Lebesgue space  (.

Theorem 2. If the sequence  satisfies the conditions (2) and (3), the following estimates

;

;

                                                      .                                                (4)                 

hold.

3. Nontangential convergence.

Тheorem 3. If  f ∈ L,  the sequence  satisfies (2), (3) and

                                                                 ,                                            

 then  the relation                                                                       

                                                          =                                                   

holds almost everywhere.

This theorem can be proved by the standard method ([2], vol. 2, pp. 464-465) due to the estimate  (4).

4. Exponential means.  Denote now

,     =,

where  ,   and require the following conditions:

А) ;  

         В) () and || decrease to zero as x increases.

Note that

                                      .

and apply twice the  Lagrange  theorem to the second finite differences in (3).

Under the conditions of  B) the sum of (3) is majorized by a corresponding  improper integral and for implementability  of  statements  of  Theorems 1, 2, 3 it is sufficient to require

    ^.

5. Generalized Poisson-Abel means. Consider in particular the case  of , then

                                        .                                     

Corollary 1.  The statements  of  Theorems  2 and 3 are valid for generalized Poisson-Abel means

                                    = 

  for all ; the constants С  in the estimates   of -norms is .

In particular, the relation

  =,   f ∈ L  ,

(nontangential convergence of Poisson-Abel means) holds for almost all x.

 6. Exponentially-polynomial summation methods. Let now  is a polynomial function of n-th degree

; 

Corollary 2. The assertions of Theorems 2 and 3 are valid for exponentially-polynomial means

= 

 for all ; the constants С  in the estimates   of -norms  is _.